Jawz
- 1
- 1
I'm studying the work of Theo Jansen and want to derive a set of general equations for motion, velocity and acceleration at each point of his linkage mechanism. I've read a general equation can be derived through the use of vector loops but I am having some trouble as my equations have 10 unknowns. I could derive equations on paper, but the brute force strategy I am thinking seems to be too much work. The pictures show my set up for each loop. I have found 5 loops for the system but have 10 unknowns. I would think there should be only 1 equation necessary since their is only 1 degree of freedom; each unknown is determined by the driving angle.
The pictures are of my work so far. First, the diagram of the system. Then, the constants and unknowns. Third, these are the vector loops from point to point. Finally, the equations are written as x and y compenents.
The angles are between the x-axis and the rod going in a counter clockwise direction.
The rod lengths are denoted as l, m, and a1 through a10.
Sorry if the pictures are poor in quality. I've tried to make everything as clear as possible.
I'm trying to find some way to organize these equations into a matrix then plot the motion of the system in Matlab or Octave.
Any help is appreciated.
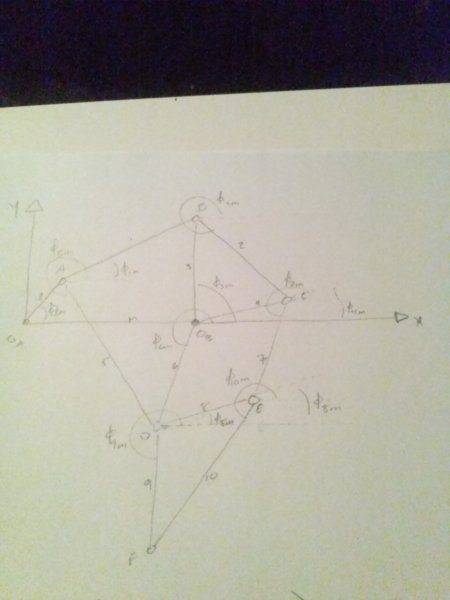
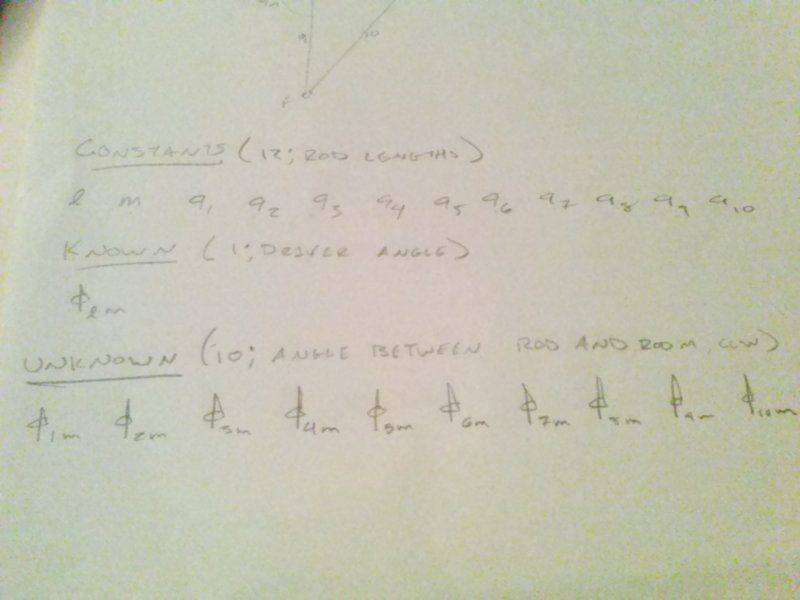
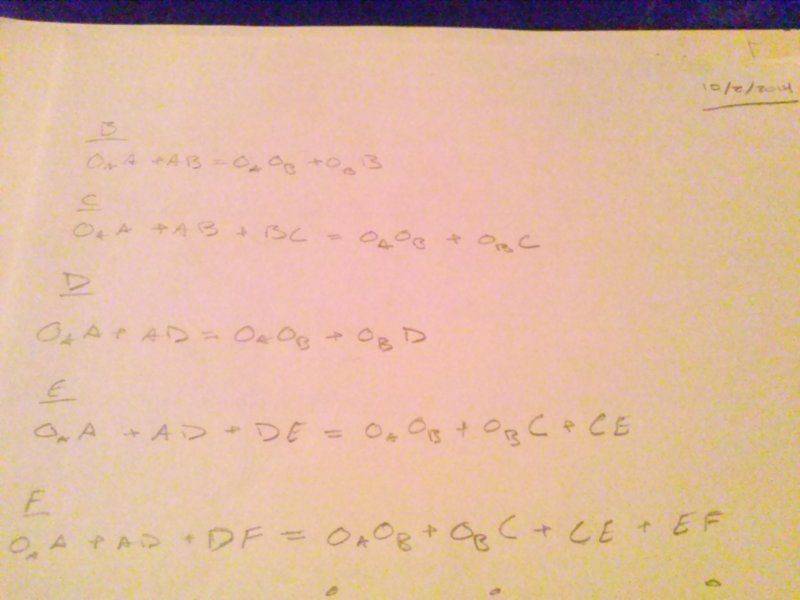

The pictures are of my work so far. First, the diagram of the system. Then, the constants and unknowns. Third, these are the vector loops from point to point. Finally, the equations are written as x and y compenents.
The angles are between the x-axis and the rod going in a counter clockwise direction.
The rod lengths are denoted as l, m, and a1 through a10.
Sorry if the pictures are poor in quality. I've tried to make everything as clear as possible.
I'm trying to find some way to organize these equations into a matrix then plot the motion of the system in Matlab or Octave.
Any help is appreciated.