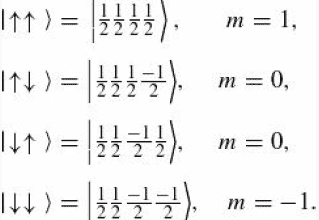pepediaz
- 49
- 5
- Homework Statement
- Each particle can have spin up or spin down, so there are four possibilities.
- Relevant Equations
- It's from Example 4.5, from Griffiths (Quantum Mechanics)
I can't why there are four elements in each ket instead of only two