jaus tail
- 613
- 48
Homework Statement
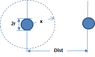
A single phase transmission line has 2 parallel conductors 1.5 metres apart. The diameter of each conductor being 0.5 cm. Calculate the line to neutral capacitance for a line 80 km long[/B]
Homework Equations
CAN = 2(3.14)(permittivity)/Loge [D/r] This gives capacitance per metre
Where D is the distance between conductors and r is the radius.
Multiplying above answer into length of line gives capacitance
The Attempt at a Solution
D = 1.5 metres = 150 cm
r = radius = 0.5 / 2 = 0.25 cm
Substituting in above equation I get CAN = 8.69 * 10-12 F / m
Multiplying this with 80 km or 80,000 m I get 0.69 micro farad.
Book answer is 3.48 micro farad
I guess they've used formula for line capacitance CAB instead of line to neutral capactiance.