bdvjofrni
- 2
- 0
I'm considering two identical spherical conductor each of radius ##a## and separated by a distance ##d##, and trying to figure out the capacitance of this configuration.
My thoughts are that since capacitance is
$$C=\frac {Q}{V}$$
and that the spherical conductors are equipotential surfaces, ##V## would just be
$$V=V_1-V_2=(\frac {kq}{a} - \frac {kq}{a+d})- (- \frac {kq}{a} + \frac {kq}{a+d}) = 2kq (\frac{1}{a} - \frac{1}{a+d})$$
and thus the capacitance would just be
$$C=\frac{1}{2k(\frac{1}{a}-\frac{1}{a+d})}=2πεa \frac {a+d}{d}$$
And then I read Wikipedia, and what I did turns out to be incorrect. Wikipedia says that the correct formula is
$$C=2πεa \sum\limits_{n=1}^∞ {\frac {\sinh (\ln (D+\sqrt {D^2-1}))}{\sinh (n \ln (D+\sqrt {D^2-1}))}}$$
I only know some very basic physics and this expression looks scary to me, but when ##a \ll d## they give pretty much the same result.
If I graph ##C## vs ##d## with a fixed radius ##a=1##, it looks like:
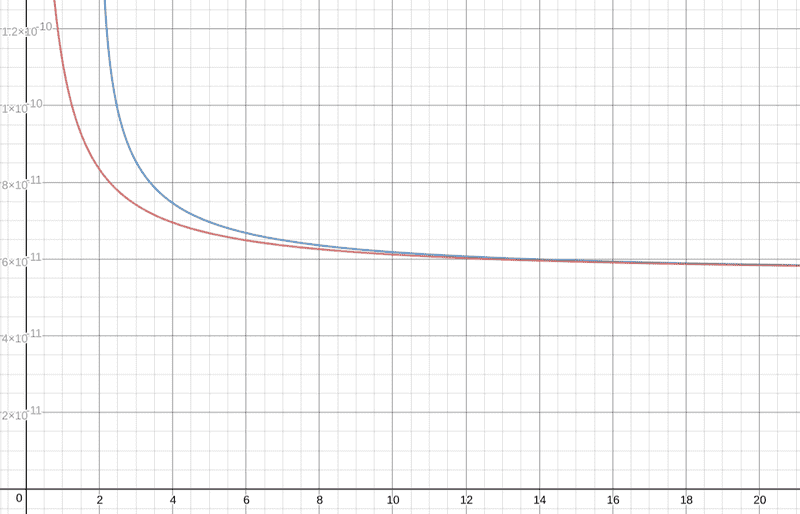
The blue line is the graph of the correct formula while red one is mine. It seems that when the separation ##d## is 10 times as big as radius ##a##, the formula I derived yields a result very close to the correct one.
So my question is, what did I fail to take into account when I considered this that led to my incorrect conclusion, and why is it that the formula I get approximately equals the correct formula when the separation gets large? (physically, not mathematically; I can see that both formulas approach horizontal asymptote ##2πεa##.
(I don't expect to really understand the correct formula on Wikipedia; that seems scary. Just wanted to know what I failed to take into account)
Thanks!
My thoughts are that since capacitance is
$$C=\frac {Q}{V}$$
and that the spherical conductors are equipotential surfaces, ##V## would just be
$$V=V_1-V_2=(\frac {kq}{a} - \frac {kq}{a+d})- (- \frac {kq}{a} + \frac {kq}{a+d}) = 2kq (\frac{1}{a} - \frac{1}{a+d})$$
and thus the capacitance would just be
$$C=\frac{1}{2k(\frac{1}{a}-\frac{1}{a+d})}=2πεa \frac {a+d}{d}$$
And then I read Wikipedia, and what I did turns out to be incorrect. Wikipedia says that the correct formula is
$$C=2πεa \sum\limits_{n=1}^∞ {\frac {\sinh (\ln (D+\sqrt {D^2-1}))}{\sinh (n \ln (D+\sqrt {D^2-1}))}}$$
I only know some very basic physics and this expression looks scary to me, but when ##a \ll d## they give pretty much the same result.
If I graph ##C## vs ##d## with a fixed radius ##a=1##, it looks like:
The blue line is the graph of the correct formula while red one is mine. It seems that when the separation ##d## is 10 times as big as radius ##a##, the formula I derived yields a result very close to the correct one.
So my question is, what did I fail to take into account when I considered this that led to my incorrect conclusion, and why is it that the formula I get approximately equals the correct formula when the separation gets large? (physically, not mathematically; I can see that both formulas approach horizontal asymptote ##2πεa##.
(I don't expect to really understand the correct formula on Wikipedia; that seems scary. Just wanted to know what I failed to take into account)
Thanks!
Attachments
Last edited:
