- #1
Louis Fry
- 10
- 1
Dear all,
I am trying to find the capacitance of a parallel plate structure that comprises a spatially varying (linear) dielectric in one dimension. I have two methods of solving this which give different answers, and I am not sure which is correct.
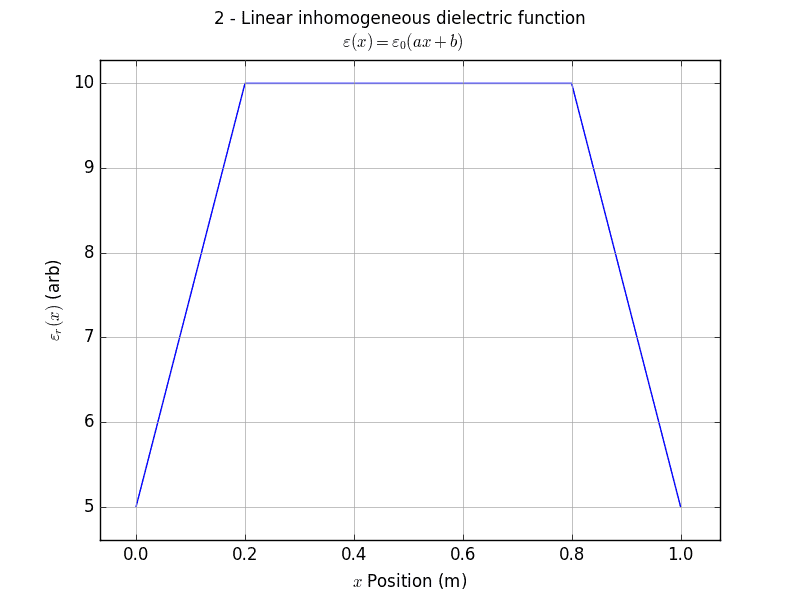
I consider the dielectric region to be free of excess charge, and therefore I took the governing equation to be \nabla \cdot \varepsilon \nabla \varphi = 0 which can be expanded to read \nabla^2 \varphi + \nabla \varphi \cdot \frac{\nabla \varepsilon}{\varepsilon} = 0 which in one dimension then reads \frac{d^2 \varphi}{dx^2} + \frac{1}{\varepsilon} \frac{d \varphi}{dx} \frac{d \varepsilon}{dx} = 0 Now I choose the functional form of \varepsilon (x), where I have split the dielectric into three regions between x_A,x_{A'},x_{B'} and x_B, shown in the attached image 'inhomogeneous_dielectric.png'. I choose the permittivity to be of the form \varepsilon(x) = \varepsilon_0 (ax + b) in the regions from x_A to x_{A'} and x_{B'} to x_B, and constant between x_{A'} and x_{B'} (the middle region). a,b are different for each side region.
In the region of constant permittivity, I use Laplace's equation as usual \frac{d^2 \varphi}{dx^2} = 0 which between x_{A'} and x_{B'} gives the expected solution of the form \varphi_{A'B'}(x) = cx + d where c and d can be determined by imposing continuity of the potential later on.
Now looking at the side regions, I get \frac{1}{\varepsilon} \frac{d \varepsilon}{dx} = \frac{1}{\varepsilon_0 (ax + b)} \frac{d}{dx}(\varepsilon_0 (ax + b)) = \frac{a}{ax + b} which leads to a differential equation of the form \frac{d^2 \varphi}{dx^2} + \frac{a}{ax + b} \frac{d \varphi}{dx} = 0
At first glance, it seems that the most obvious solution is of the form \varphi_{AA'}(x) = \pm \ln(ax + b) however this is not very useful since there is no way of controlling the shape of this equation to match the potential at the outer boundaries \varphi_A and \varphi_B (V = \varphi_B-\varphi_A). Then I notice that a more general solution is in fact \varphi_{AA'}(x) = c_1 \ln(ax + b) + c_2 which is now in a form that can be controlled.
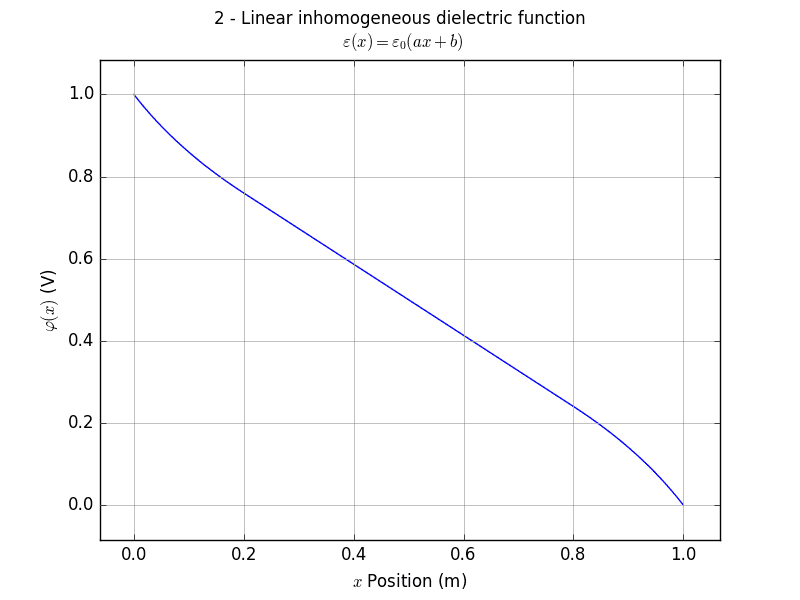
This leads to six unknowns, which can be solved using six boundary conditions, ie that the potentials match at the outer and inner boundaries, and that the potential is smooth across each inner boundary. This appears to work ok, the result is shown in 'potential_profile.png' for V = 1V.
Then I calculate the electric flux density in each region using D(x) = -\varepsilon(x)\frac{d\varphi}{dx} which yields a constant flux density throughout the structure from points A to B. This suggests this is the correct solution for the potential. The charge on each plate is then determined from Q = AD where A is the junction area.
Now for the two methods of calculating the capacitance:
1 - Using the flux density and potentials in each region:
The total capacitance is described as \frac{1}{C_t} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} where the capacitance in each region is calculated as C_i = A \frac{D}{V_i} where each of V_i are the potential differences across each region, calculated using the potential solution in each region.
Using this method I get C_t/A \approx 7.67 \times 10^{-11} \mathrm{F.m^{-2}} which gives an effective dielectric constant of \varepsilon_{eff} = C_t (x_B - x_A)/A \approx 8.66 \varepsilon_0
2 - Using a 'macroscopically averaged' permittivity:
Using this method avoids solving for the potential, however the result obtained is a little larger. The average dielectric constant throughout the structure is computed as \varepsilon_{avg} = \frac{1}{x_B - x_A} \int_{x_A}^{x_B} \varepsilon(x) dx which with the present values gives \varepsilon_{avg} = 9\varepsilon_0. I then calculate the capacitance as C_t = \varepsilon_{avg} \frac{A}{x_B - x_A} which gives the result C_t/A \approx 7.97 \times 10^{-11} \mathrm{F.m^{-2}} which is arguably similar to the above method, but slightly larger.
I would go with method 1, since the whole system is solved in that case, however I don't see where the discrepancy comes from. Does anyone have any ideas?
Thanks for reading!
I am trying to find the capacitance of a parallel plate structure that comprises a spatially varying (linear) dielectric in one dimension. I have two methods of solving this which give different answers, and I am not sure which is correct.
I consider the dielectric region to be free of excess charge, and therefore I took the governing equation to be \nabla \cdot \varepsilon \nabla \varphi = 0 which can be expanded to read \nabla^2 \varphi + \nabla \varphi \cdot \frac{\nabla \varepsilon}{\varepsilon} = 0 which in one dimension then reads \frac{d^2 \varphi}{dx^2} + \frac{1}{\varepsilon} \frac{d \varphi}{dx} \frac{d \varepsilon}{dx} = 0 Now I choose the functional form of \varepsilon (x), where I have split the dielectric into three regions between x_A,x_{A'},x_{B'} and x_B, shown in the attached image 'inhomogeneous_dielectric.png'. I choose the permittivity to be of the form \varepsilon(x) = \varepsilon_0 (ax + b) in the regions from x_A to x_{A'} and x_{B'} to x_B, and constant between x_{A'} and x_{B'} (the middle region). a,b are different for each side region.
In the region of constant permittivity, I use Laplace's equation as usual \frac{d^2 \varphi}{dx^2} = 0 which between x_{A'} and x_{B'} gives the expected solution of the form \varphi_{A'B'}(x) = cx + d where c and d can be determined by imposing continuity of the potential later on.
Now looking at the side regions, I get \frac{1}{\varepsilon} \frac{d \varepsilon}{dx} = \frac{1}{\varepsilon_0 (ax + b)} \frac{d}{dx}(\varepsilon_0 (ax + b)) = \frac{a}{ax + b} which leads to a differential equation of the form \frac{d^2 \varphi}{dx^2} + \frac{a}{ax + b} \frac{d \varphi}{dx} = 0
At first glance, it seems that the most obvious solution is of the form \varphi_{AA'}(x) = \pm \ln(ax + b) however this is not very useful since there is no way of controlling the shape of this equation to match the potential at the outer boundaries \varphi_A and \varphi_B (V = \varphi_B-\varphi_A). Then I notice that a more general solution is in fact \varphi_{AA'}(x) = c_1 \ln(ax + b) + c_2 which is now in a form that can be controlled.
This leads to six unknowns, which can be solved using six boundary conditions, ie that the potentials match at the outer and inner boundaries, and that the potential is smooth across each inner boundary. This appears to work ok, the result is shown in 'potential_profile.png' for V = 1V.
Then I calculate the electric flux density in each region using D(x) = -\varepsilon(x)\frac{d\varphi}{dx} which yields a constant flux density throughout the structure from points A to B. This suggests this is the correct solution for the potential. The charge on each plate is then determined from Q = AD where A is the junction area.
Now for the two methods of calculating the capacitance:
1 - Using the flux density and potentials in each region:
The total capacitance is described as \frac{1}{C_t} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} where the capacitance in each region is calculated as C_i = A \frac{D}{V_i} where each of V_i are the potential differences across each region, calculated using the potential solution in each region.
Using this method I get C_t/A \approx 7.67 \times 10^{-11} \mathrm{F.m^{-2}} which gives an effective dielectric constant of \varepsilon_{eff} = C_t (x_B - x_A)/A \approx 8.66 \varepsilon_0
2 - Using a 'macroscopically averaged' permittivity:
Using this method avoids solving for the potential, however the result obtained is a little larger. The average dielectric constant throughout the structure is computed as \varepsilon_{avg} = \frac{1}{x_B - x_A} \int_{x_A}^{x_B} \varepsilon(x) dx which with the present values gives \varepsilon_{avg} = 9\varepsilon_0. I then calculate the capacitance as C_t = \varepsilon_{avg} \frac{A}{x_B - x_A} which gives the result C_t/A \approx 7.97 \times 10^{-11} \mathrm{F.m^{-2}} which is arguably similar to the above method, but slightly larger.
I would go with method 1, since the whole system is solved in that case, however I don't see where the discrepancy comes from. Does anyone have any ideas?
Thanks for reading!