Capillary action meniscus height in a tube fitted inside another tube?

[Alfred1]

Hello,

I was thinking about how would capillary action change in a tube (classic example) and in a tube fitted inside another tube (considering water as the liquid involved).

This is no homework question, it's just a thought which striked my mind but I don't have sufficient basic knowledge to solve. Feel free to move it if you think it may be more appropriate there or it gets more chances to get answered.

Height of liquid column:

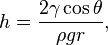
where:

γ = liquid-air surface tension
θ = contact angle
ρ = density of liquid
g = gravity acceleration
r = radius


I tried my best to draw the examples I'm interested in order to help my explanation.

I didn't consider the capillarity inside the smaller tube in both example #2 and #3 because I'd like to assume that "a/2" in example #1 is close to "c" in example #2 and #3 (drawings not to scale).

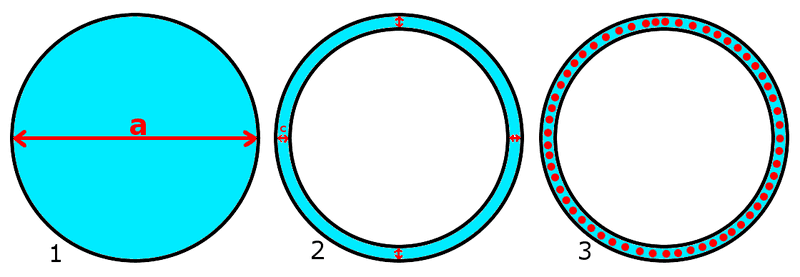
Since from what I understand the column height is given, among other things (most of which can't be changed, like liquid-air surface tension, contact angle, density of liquid and gravity acceleration), by the tube radius, I'd like to know if "c" in example #2 can be considered as "a/2" in example #1 to calculate column height using above formula.

Also I'd like to know how having beads of slightly smaller diameter than "c" between the two tubes (example #3) would affect the column height.

If said beads were less dense than water, could they still improve column height or would they just form a floating mat on top of 1 unit thickness?

What'd be the column height of example #2 and #3 assuming "c" as 1mm ?

I'm quite sure that given the same reached height "h" in example #2 and #3, "c" of #2 has to be smaller than "c" in #3.


Thank you very much

 

[A.T.]

Height of liquid column:

where:

γ = liquid-air surface tension
θ = contact angle
ρ = density of liquid
g = gravity acceleration
r = radius

Here is an interesting point on this:
http://www.lps.ens.fr/~balibar/Caupin-EPL08.pdf

It has already been seen experimentally that the capillary
rise in small (wetting) pores exceeds the prediction
from Jurin’s law [3]. Such behavior is understood to arise
from the fact that a wetting film reduces the effective value
of R, the radius of curvature of the meniscus [3].

If said beads were less dense than water, could they still improve column height or would they just form a floating mat on top of 1 unit thickness?

Maybe if the beads would stick to the walls and transfer vertical forces to it.

 

[Alfred1]

Here is an interesting point on this:
http://www.lps.ens.fr/~balibar/Caupin-EPL08.pdf

Maybe if the beads would stick to the walls and transfer vertical forces to it.

Thanks for your reply :)

Do you know how'd Jurin's law change according to example #2 and #3 ?

What'd be the column height of example #2 and #3 assuming "c" as 1mm ?

Slightly guessed results would still be better than nothing since I lack the basics to guess this myself.

Thank you all