Capillary Force in a V shaped tube

[dpage]

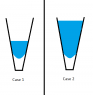
Suppose we have a very small V shaped tube-like vessel that is closed at the bottom (see attached picture).

Question 1:
If a drop of liquid enters the vessel from the top, what determines the stopping point of the drop (i.e. at what point is the force of gravity countered and the drop stops...?). I imagine this equation would include the radius of the tube at any given vertical value, along with the contact angle of the liquid with the solid...Is there such an equation?

Question 2:
Suppose you have added a drop as described in question 1, but after the drop stops moving down you add more liquid on top. Will the drop sink further down the hole as a function of how much liquid is in the vessel?

The attached figure depicts questions 1 and 2 as Case 1 and Case 2, respectively.
thanks

 

[Andy Resnick]

This problem is directly related to the recovery of oil and gas from the ground- the oil must flow through pores in the rock. The relevant parameters are the contact angle the liquid makes with the glass and the interfacial energy between the liquid and gas.

The starting point is Laplace's equation $\Delta P = -\sigma\kappa$, where $\Delta P$ is the pressure jump across the liquid-gas interface, $\sigma$ the interfacial energy, and $\kappa$ the curvature of the interface. The curvature of the interface is constrained by the contact angle, although for small lengths (small pore sizes) the shape is close to a section of a sphere, so the curvature is approximately 2/r, where r is the radius of the sphere. This radius is not generally the radius of the pore diameter, but is found by determining the contact angle. Thus, fluids that wet the solid can penetrate further (or through smaller pores) than non-wetting fluids.