DivGradCurl
- 364
- 0
Hi all,
I'm reviewing device physics and I would like to understand how majority and minority carrier concentrations for both N- and P-type substrates change with temperature. My reference, Pierret's Semiconductor Device Fundamentals, has this figure:
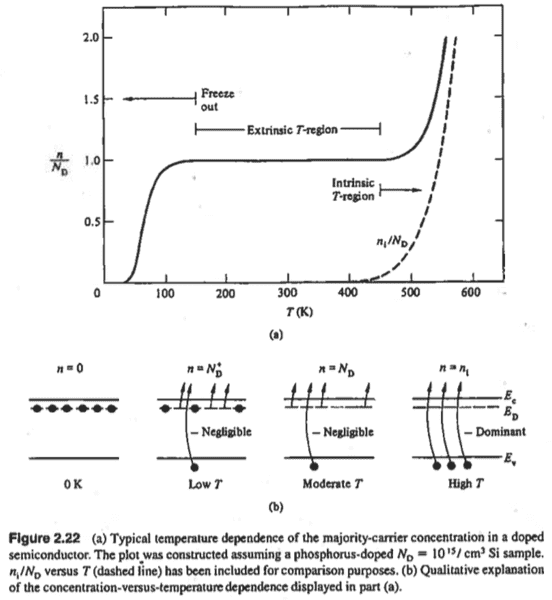
and I want to generate curves for all cases. However, I'm only given these equations

which only seem to cover the extrinsic and intrinsic regions; it doesn't work for "freeze out". Here is what I get using the "n, p, and Fermi Level Computational Relationships":
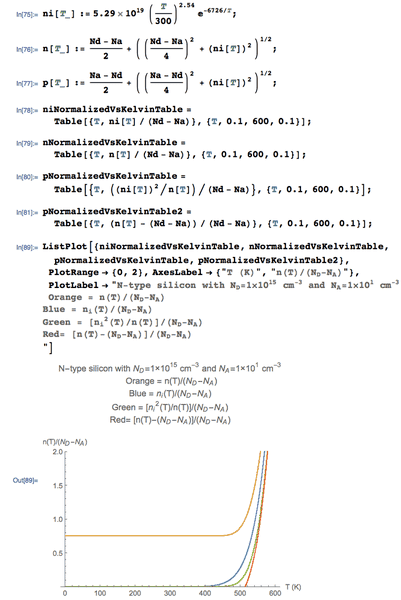
Mathematica notebook download link:
https://drive.google.com/open?id=0ByhrqgHUHYVjaVdHM3UwNUlWSHc
which obviously does not match the figure above. I also wonder how the characteristic looks like for minority carriers, and I would like to repeat the figure for the P-type substrate case.
I checked a number of references, but could not find expressions that yield the desired result. I did find a figure generated in Silvaco ATLAS:
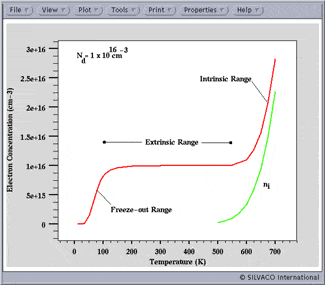
Article:
http://www.silvaco.com/tech_lib_TCAD/simulationstandard/2000/nov/a1/a1.html
However, the calculation is not explained, which makes sense; it's a commercial software. It seems that the "freeze out" region is not simple to calculate as I could not find expressions in books. It appears to me that the carrier effective mass is a function of temperature, but books provide only 300K values, and that may be necessary if the correct expressions for the general case are those that rely on integrals and effective masses.
Can someone explain this? A hand-drawn sketch explaining the majority and minority carrier concentration as a function of temperature for both N- and P-type Si would be fine, if you happen to understand all cases. If you also know what's going wrong with my calculation, also let me know.
Thanks!
I'm reviewing device physics and I would like to understand how majority and minority carrier concentrations for both N- and P-type substrates change with temperature. My reference, Pierret's Semiconductor Device Fundamentals, has this figure:
and I want to generate curves for all cases. However, I'm only given these equations
which only seem to cover the extrinsic and intrinsic regions; it doesn't work for "freeze out". Here is what I get using the "n, p, and Fermi Level Computational Relationships":
Mathematica notebook download link:
https://drive.google.com/open?id=0ByhrqgHUHYVjaVdHM3UwNUlWSHc
which obviously does not match the figure above. I also wonder how the characteristic looks like for minority carriers, and I would like to repeat the figure for the P-type substrate case.
I checked a number of references, but could not find expressions that yield the desired result. I did find a figure generated in Silvaco ATLAS:
Article:
http://www.silvaco.com/tech_lib_TCAD/simulationstandard/2000/nov/a1/a1.html
However, the calculation is not explained, which makes sense; it's a commercial software. It seems that the "freeze out" region is not simple to calculate as I could not find expressions in books. It appears to me that the carrier effective mass is a function of temperature, but books provide only 300K values, and that may be necessary if the correct expressions for the general case are those that rely on integrals and effective masses.
Can someone explain this? A hand-drawn sketch explaining the majority and minority carrier concentration as a function of temperature for both N- and P-type Si would be fine, if you happen to understand all cases. If you also know what's going wrong with my calculation, also let me know.
Thanks!

