Center of Mass of open top cylinder

[naianator]

Homework Statement

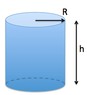
The attached diagram shows a uniform density hollow cylindrical shell with a solid bottom and an open top. It has radius R and height h.

Find the height for the center of mass of this cylinder, taking the origin of the coordinate system at the center of the bottom. Use "pi" for π.

Homework Equations

x_cm=m_1x_1+m_2x_2+m_3x_3/m_1+m_2+m_3

The Attempt at a Solution

I'm not even really sure how to start but I tried this

If the top wasn't missing then the cylinder would have a center of mass at h/2 and the missing top has a center of mass at h so

CM = (h/2*(2*pi*R*h+2*pi*R^2)-h*pi*R^2)/2*pi*R*h+2*pi*R^2-pi*R^2

= pi*R*h^2/2*pi*R*h-pi*R^2

 

[Borg]

If you had just the top piece located at height h, could you determine the center of its mass?

 

[naianator]

If you had just the top piece located at height h, could you determine the center of its mass?

Wouldn't it just be h?

 

[Borg]

Wouldn't it just be h?

And can you determine the mass of it?

 

[naianator]

And can you determine the mass of it?

Wouldn't the masses cancel though? h = h*m/m?

 

[haruspex]

CM = (h/2*(2*pi*R*h+2*pi*R^2)-h*pi*R^2)/2*pi*R*h+2*pi*R^2-pi*R^2

= pi*R*h^2/2*pi*R*h-pi*R^2

You really ought to parenthesise expressions correctly. You mean
(h/2*(2*pi*R*h+2*pi*R^2)-h*pi*R^2)/(2*pi*R*h+2*pi*R^2-pi*R^2)
or in LaTex
$\frac{\frac h2(2\pi Rh+2\pi R^2)-h\pi R^2}{2\pi Rh+2\pi R^2-\pi R^2}$
But you made a mistake in simplifying to
$\frac{\pi Rh^2}{2\pi R h-\pi R^2}$
(Note that that would make it > h/2.)

 

[naianator]

You really ought to parenthesise expressions correctly. You mean
(h/2*(2*pi*R*h+2*pi*R^2)-h*pi*R^2)/(2*pi*R*h+2*pi*R^2-pi*R^2)
or in LaTex
$\frac{\frac h2(2\pi Rh+2\pi R^2)-h\pi R^2}{2\pi Rh+2\pi R^2-\pi R^2}$
But you made a mistake in simplifying to
$\frac{\pi Rh^2}{2\pi R h-\pi R^2}$
(Note that that would make it > h/2.)

I'm having trouble finding where the mistake is. Is the first expression correct?

 

[haruspex]

I'm having trouble finding where the mistake is. Is the first expression correct?

Yes, it's just the last line that's wrong. Check the signs.

 

[naianator]

Yes, it's just the last line that's wrong. Check the signs.

Ahhh yes! Thank you

 

[SammyS]

If the top wasn't missing then the cylinder would have a center of mass at h/2 and the missing top has a center of mass at h so

Rather than that:

If both the top and bottom were missing, then the CM would be at h/2.

To this add in the bottom, which has CM at 0 .

It makes the algebra a bit easier.