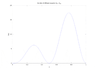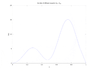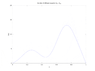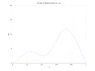
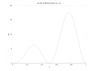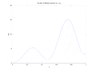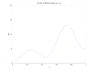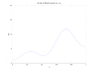
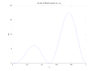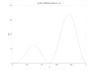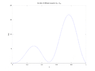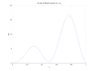
The diffusion equation dS/dt = Ds (d^2S/dx^2)
Which has the following Central Difference Solution
S(i,j+1) = S(i,j) + (dt/dx^2)*Ds*(S(i+1,j) - 2*S(i,j) + S(i-1,j));
I would like Neumann Boundary conditions at each end. That is, dS/dx = 0.
To obtain an equation for this, we look at the central difference approximation to dS/dx, which is:
(S i+1 - S i-1) / dx^2
For the case where i =1 (first node in the x direction), we get the following:
[S(2)-S(0)] / dx^2 = 0. Therefore S(0) = S(2).
Thus, the second derivative central difference now becomes,
d^2S / dx^2 = 2(S(2) - S(1)) / dx^2
This is implemented in MatLab as a boundary condition of
S(1,1) = 2*(S(i,j)-S(i-1,j))./dx.^2;
Simularly, at a i = numx, S(numx+1) = S(numx-1), so we have
S(numx,1) = 2*(S(numx-1,j)-S(numx,j))./dx.^2;
Therefore, my boundary conditions are the following:
S(1,1) = 2*(S(i,j)-S(i-1,j))./dx.^2;
S(numx,1) = 2*(S(numx-1,j)-S(numx,j))./dx.^2;