SUMMARY
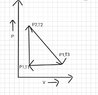
The discussion centers on the calculation of heat transfer (ΔQ) and internal energy change (ΔU) in thermodynamic processes involving ideal gases. The specific heat capacity used in the calculations is Cv, as internal energy for an ideal gas is solely a function of temperature. The work done by the gas (ΔW) can be determined using the trapezium area under the pressure-volume curve. The overall change in internal energy for a complete cycle is zero, as the system returns to its initial state.
PREREQUISITES
- Understanding of thermodynamic principles, particularly the first law of thermodynamics.
- Familiarity with ideal gas laws, specifically PV = nRT.
- Knowledge of specific heat capacities, particularly Cv and Cp.
- Ability to calculate areas under curves in pressure-volume diagrams.
NEXT STEPS
- Study the derivation of the first law of thermodynamics and its applications.
- Learn how to calculate work done in thermodynamic processes using pressure-volume diagrams.
- Explore the differences between Cv and Cp in various thermodynamic scenarios.
- Investigate the implications of internal energy changes in cyclic processes for ideal gases.
USEFUL FOR
This discussion is beneficial for students and professionals in thermodynamics, mechanical engineers, and anyone involved in the study of heat transfer and energy systems.