Change in Internal Energy in Accelerated Gas Chambers

AI Thread Summary
The discussion focuses on how internal energy changes in two toroidal gas chambers under angular acceleration, with one chamber featuring an adiabatic partition. Participants are seeking clarity on the insulation of the torus, the viscosity of the gas, and whether the comparison is qualitative. The problem involves calculating the change in internal energy per second for both chambers as they accelerate. There is an analogy drawn to linear motion in gas cabins during acceleration. The conversation highlights the need for a structured approach to begin the calculations.
gianeshwar
Messages
225
Reaction score
14
Summary:: How internal energy changes in a acclerated cabin.

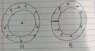
There are two tourus shaped insulated closed pipes containing equal amounts of ideal gas under same conditions.
B has a adiabatic partion wall.
If both are to change angular velocity by w radians per second.
How internal energies will change in both?
 

Attachments

  • IMG_20210109_120438.jpg
    IMG_20210109_120438.jpg
    50.5 KB · Views: 171
Physics news on Phys.org
What are your thoughts on this so far? Is the torus insulated? Is the gas considered to have viscosity? is this supposed to be a qualitative comparison?
 
Last edited:
Chestermiller said:
What are your thoughts on this so far? Is the torus insulated? Is the gas considered to have viscosity? is this supposed to be a qualitative comparison?
Sorry for hurridly writing the question .Here , w is angular acceleration of taurus w.r.t a perpendicular axis to plane of taurus through centre. Ignore viscus drag.
I need to calculate change in internal energy per second in both cases.
Not getting idea to start.
My basis of thinking is an analogous process in linear motion of a cabin of gas when the cabin gets acclerated linearly.
 
gianeshwar said:
Sorry for hurridly writing the question .Here , w is angular acceleration of taurus w.r.t a perpendicular axis to plane of taurus through centre. Ignore viscus drag.
I need to calculate change in internal energy per second in both cases.
Not getting idea to start.
My basis of thinking is an analogous process in linear motion of a cabin of gas when the cabin gets acclerated linearly.
What is the exact word-for-word statement of this problem?
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Change in internal energy of a cylinder
Replies
8
Views
2K
Internal Energy of an Ideal Gas
Replies
4
Views
2K
Deriving an expression for change in internal energy
Replies
5
Views
1K
Internal energy during the expansion of a gas?
Replies
3
Views
2K
Is the change in internal energy really a state function?
Replies
4
Views
1K
Work done in a chamber with gas undergoing adiabatic free expansion?
Replies
13
Views
2K
Thermodynamics: Internal Energy, Heat and Work Problem
Replies
1
Views
2K
How Is Internal Energy Calculated for an Ideal Gas Using Temperature Change?
Replies
1
Views
1K
Internal energy of a container filled with water & steam
Replies
12
Views
2K
Change In Internal Energy Of An Ideal Gas
Replies
14
Views
7K

Hot Threads

Recent Insights

Back
Top