Changing Momentum: Unpacking the Confusion

[PhysicsKid0123]

[Mentor's note: This post does not use the homework-forums template because it was originally posted in one of the discussion forums. I moved it here instead of deleting it because it already had several answers in the spirit of the homework-forum rules.]

Okay so I am having a hard time wrapping my head around this. Before looking at the answer I worked the example and got the answer only because I used dimensional analysis to get me to the right units for force. However, to be honest, I don't think I even understand the concept here. I know mass is changing and velocity is constant, but what is throwing me off is where it says "The water strikes the window at 32 m/s so each kilogram of water loses 32 kg.m/s of momentum. Water strikes the window at the rate of 45 kg/s, so the rate at which it loses momentum to the window is... 1400kg m/s^2" How is it losing 32 kg m/s of momentum and then at the same time also losing it at a rate of 1400 kg m/s^2? Why does it even mention "The water strikes the window at 32 m/s so each kilogram of water loses 32 kg.m/s of momentum" what is the purpose of that sentence. That is really confusing me.

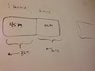
I added this simple diagram to show how I see this system. Where is 32 kg. m/s of momentum come in? (I am aware that the window is now showing)

 

[Drakkith]

This should be posted in the homework section, but give me a minute to go over it and I'll see if I can help while I eat my egg sandwich.

 

[Drakkith]

Okay, each kg of water has 32 kg m/s of momentum, as you've written above the box.
Now, how much water is striking the window per second?

 

[PhysicsKid0123]

45kg per second...

 

[Drakkith]

Okay. So we have water traveling at 32 m/s, with a momentum of 32 kg m/s per kg of water. We also have 45 kg of water striking the window every second.

To put this in other words, if I take 1 kg of water and throw it against the window at 32 m/s it will lose 32 kg m/s of momentum since the window completely stops it. But I'm not throwing just one of these 1 kg blocks of water, I'm throwing 45 of them per second. So how much momentum is the water losing per second?

Note that we do NOT have a change in mass anywhere in the problem.

 

[PhysicsKid0123]

okay I see it would lose 1440 kg m/s^{2}

So to summarize, 1 kg chunk thrown at 32m/s is losing 32 kg m/s of momentum, but since we are throwing 45 of them per second, we are losing a total of 1440 kg m/s of momentum, and yet again, this loss of momentum happens every second.

That is my understanding. Is that right? I think I understand now.

 

[PhysicsKid0123]

So there isn't any calculus involved here then, right?

 

[sophiecentaur]

So there isn't any calculus involved here then, right?

Calculus is always there. It's just that some problems can make the calculus so trivial that we don't explicitly use it. Look upon force as Rate of Change of Momentum - that's calculus, isn't it? The rate of change of momentum, in this case, is constant (velocity change times rate of mass arriving). So you have your answer.
You did this sum without involving specific integration or differentiation but there are many examples (like rockets) where the masses are changing all the time and calculus rears its head and you need to do some integration.