donpacino
Science Advisor
Gold Member
- 1,439
- 285
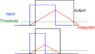
no. the equation is not linear.Seth Cohen said:Agreed, I can tune RC or I can tune the threshold ob the comparator to adjust m.
run a test for me. use a very small pulse width with your compactor setup
then use a very long pulse width with your comparator.
evaluate what the gains are. it will not be linear
make sure with the long pulse width you do not saturate your output voltage.