- #1
chwala
Gold Member
- 2,697
- 360
- TL;DR Summary
- see attached.
My interest is on the highlighted part only...my understanding is that one should use simultaneous equation... unless there is another way hence my post query.
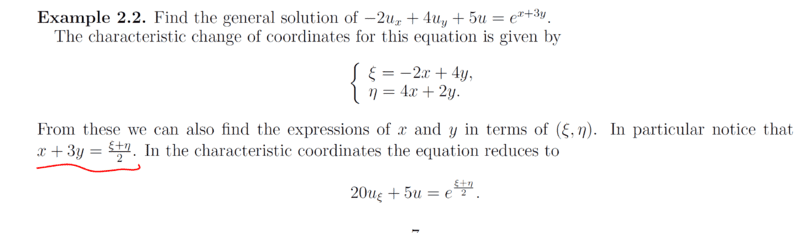
In my working i have;
##y=\dfrac{2ξ+η}{10}## and ##x=\dfrac{2η-ξ}{10}## giving us;
##x+3y=\dfrac{2η-ξ+6ξ+3η}{10}=\dfrac{5ξ+5η}{10}=\dfrac{ξ+η}{2}## cheers guys.
In my working i have;
##y=\dfrac{2ξ+η}{10}## and ##x=\dfrac{2η-ξ}{10}## giving us;
##x+3y=\dfrac{2η-ξ+6ξ+3η}{10}=\dfrac{5ξ+5η}{10}=\dfrac{ξ+η}{2}## cheers guys.