Clashing approximations for this precession problem

[etotheipi]

I have a bit of a strange puzzle I can't work out. Let's say, we have a thin cylindrical disk of mass $m$ and radius $r$ connected on one side to a light axle of length $d$ through its centre. The axle is itself connected to a light string of length $l$, the other end of which is connected to a fixed point. The string is taut and makes an angle of $\theta$ to the downward vertical, whilst the axle is horizontal and points in the radial direction, like this:

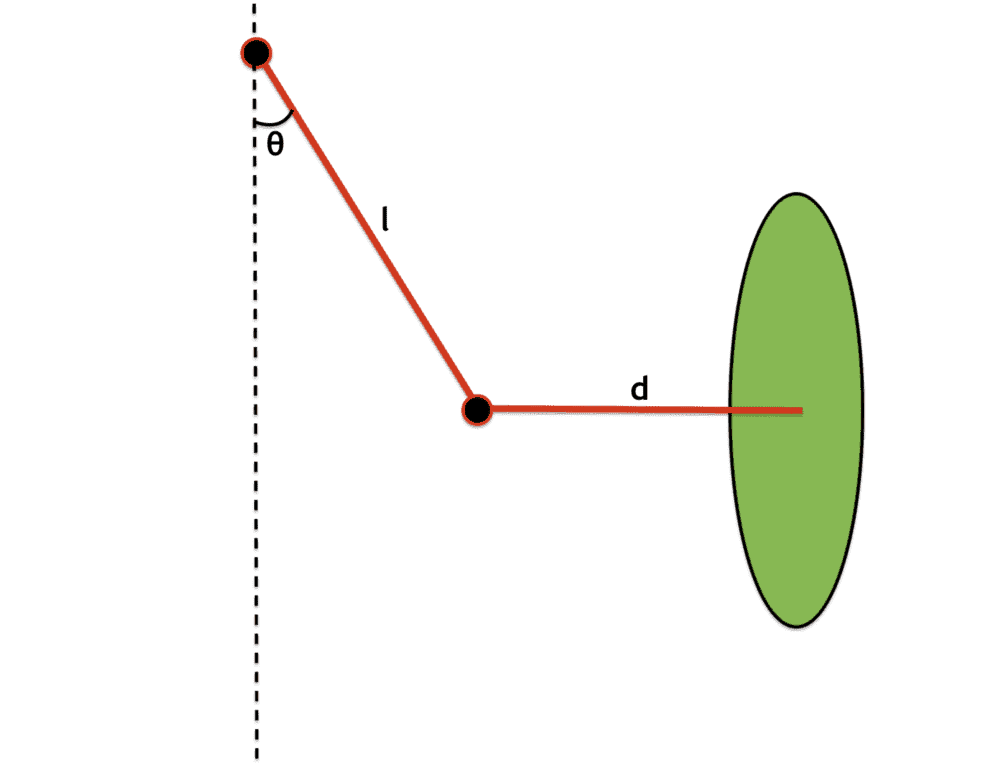
If the disk spins about its own central axis at $\boldsymbol{\omega} = \omega_S \boldsymbol{e}_r$, and the configuration precesses about the dotted axis at $\boldsymbol{\Omega} = \Omega_z \boldsymbol{e}_z$, then under the usual gyroscopic approximations $\omega_S \gg \Omega_z$ and $d\Omega_z/dt = d\omega_S/dt = 0$, we want to determine $\Omega_z$.

One way to solve it might be to take a coordinate system with origin at the hinge at the very top left hinge, and consider the system to be the string + rod + disk, in which case the angular momentum of the configuration is$$\mathbf{L} = \frac{1}{2}mr^2 \omega_S \boldsymbol{e}_r + [m(l\sin{\theta} + d)^2\ + \frac{1}{4}mr^2] \Omega_z \boldsymbol{e}_z \, \,

\overset{\text{gyro approx}}{\implies} \, \, \boldsymbol{\tau} = (l\sin{\theta} + d)mg \boldsymbol{e}_{\theta} = \frac{1}{2}mr^2 \omega_s \Omega_z \boldsymbol{e}_{\theta}
$$where the equality on the right equation holds under the approximation that $d\Omega_z / dt = 0$. Another way to solve it, however, would be to take a coordinate system with origin at the centre of the disk (translating with the disk, but not rotating with the disk - i.e. as viewed by this coordinate system, the disk is slowly rotating about its own vertical axis), and consider the system to be the rod + disk. In this analysis, then, the string tension $T$ is an external force. In this coordinate system the angular momentum of the system is$$\boldsymbol{L} = \frac{1}{2}mr^2 \omega_S \boldsymbol{e}_r + \frac{1}{4} mr^2 \Omega_z \boldsymbol{e}_z \quad \overset{\text{gyro approx}}{\implies} \quad \boldsymbol{\tau} = dT\cos{\theta} \boldsymbol{e}_{\theta} = dmg \boldsymbol{e}_{\theta} = \frac{1}{2}mr^2 \omega_s \Omega_z \boldsymbol{e}_{\theta}$$where we used that $F_z = T\cos{\theta} - mg = 0$. This second approach implies that the precession speed has no dependence on the string length nor the angle.

I presumed that, if I didn't mess up anywhere (I mean, it's pretty likely that I did! ), the discrepancy has to do with the assumptions made. Can anyone see? Thanks!

 

[A.T.]

...the discrepancy ...

What is the discrepancy exactly? Your final terms look the same.

 

[etotheipi]

What is the discrepancy exactly? Your final terms look the same.

The first approach gives$$\Omega_z = \frac{2g(l\sin{\theta} + d)}{r^2 \omega_s}$$whilst the second approach gives$$\Omega_z = \frac{2gd}{r^2 \omega_s}$$Apparently, the second answer is the correct one! I wonder if, the gyroscopic approximation only holds if $\theta= 0$...

 

[vanhees71]

It's not clear to me, what the precise setup is. Is the angle $\theta$ fixed or not? Is the horzontally drawn rod fixed or can it rotate around the point it is fixed at the string? In any case the Lagrangian should uniquely give an equation of motion without ambiguities.

 

[etotheipi]

Oh yeah, I forgot about this problem, I figured out the resolution last night, and it was a pretty silly mistake

The issue was that the angular momentum I wrote down in the first equation (about the top left hinge) was incorrect, since one of the terms in the angular momentum should have been$$[-l\cos{\theta} \boldsymbol{e}_z + (l\sin{\theta} + d) \boldsymbol{e}_r] \times \Omega_z (l\sin{\theta} + d) \boldsymbol{e}_{\theta}$$instead of$$[(l\sin{\theta} + d) \boldsymbol{e}_r] \times \Omega_z (l\sin{\theta} + d) \boldsymbol{e}_{\theta}$$

Is the horzontally drawn rod fixed or can it rotate around the point it is fixed at the string?

The rod is rotating around with the whole configuration

I might write up the solution later for future reference, but I'm a bit embarrassed not spotting the mistake earlier!

 

[etotheipi]

Okay, so here's the tea. First of all I'll note that it's a lot easier to solve it by taking an origin at the centre of mass, or solving the variational problem with the Lagrangian.

We also note that the problem specifies $\theta$ is small, so the validity of the small angle approximation holds here. But anyway, about the top left hinge,$$\mathbf{L} = m[-l\cos{\theta} \boldsymbol{e}_z + (l\sin{\theta} + d) \boldsymbol{e}_r] \times \Omega_z (l\sin{\theta} + d) \boldsymbol{e}_{\theta} + \frac{1}{2} mr^2 \omega_s^2 \boldsymbol{e}_r + \frac{1}{4} mr^2 \Omega \boldsymbol{e}_z$$On differentiation this will then give$$\frac{d\mathbf{L}}{dt} = m(\Omega^2 l^2 \sin{\theta} \cos{\theta} + \Omega^2 l d \cos{\theta} + \frac{1}{2}mr^2 \omega_s \Omega) \boldsymbol{e}_{\theta}$$From the Newton equation $\mathbf{F} = m\ddot{\mathbf{x}}_{\mathcal{CM}}$ applied to the centre of mass we obtain, if $T$ is the tension,$$T\sin{\theta} = m(l\sin{\theta} + d)\Omega^2, \quad T\cos{\theta} = mg$$or in other words$$\tan{\theta} = \frac{1}{g} \left[ l\sin{\theta} + d \right] \Omega^2 \approx \sin{\theta} \implies mlg\sin{\theta} \approx ml^2 \Omega^2 \sin{\theta} + mld\Omega^2$$Clearly if we take $\cos{\theta} \approx 1$ then this is just what's inside the first two terms of $d\mathbf{L}/dt$, or in other words$$d\mathbf{L}/dt = mlg\sin{\theta} \boldsymbol{e}_{\theta} + \frac{1}{2} mr^2 \omega_s \Omega \boldsymbol{e}_{\theta}$$The torque is evidently$$\boldsymbol{\tau} = (l\sin{\theta} + d)mg \boldsymbol{e}_{\theta}$$and on equality we obtain$$mgd = \frac{1}{2} mr^2 \omega_s \Omega $$which is, exactly what we obtained with the other approach.

Moral of the story is don't drop terms!