How Does Time Differ for Observers in Relative Motion?

[Hepic]

Lets say that we have a spaship(with a man) that has speed,and a woman at ground that has not speed.
Man throughs a light at ground and light comes again at spaceship. For man light follow a straight line,but for woman follow a V destination.
Both see light speed to run with the same constant speed.But man see light to follow a smaller destination,so for woman man's clock run slower,but for man woman's clock run slower too.
That is clear to me.
That what I want to ask is:"Both will count the same time at their clocks. For example If man counts 2 second,what about woman?"

Sorry for my bad english.
Thanks a lot !

 

[dauto]

How do you suppose they should compare their clocks?

If the man jumps on another ship and comes back to Earth than he counts fewer seconds. If the woman jumps on a faster ship and catches up with the man than she counts fewer seconds. Other possibilities might give different results

 

[HallsofIvy]

Lets say that we have a spaship(with a man) that has speed,and a woman at ground that has not speed.

What do you mean by "has speed" and "has not speed"? In what frame of reference? Certainly there exist a frame of reference (that of the woman) in which the spaceship has speed v and the woman speed 0. But there also exist a frame of reference (that of the man) in which the spaceship has speed 0 and the woman speed v.

Man throughs a light at ground and light comes again at spaceship.

"throwing the light" stopped me for a moment! You mean the man shone a light at the woman and it was reflected back to the man.

For man light follow a straight line,but for woman follow a V destination.
Both see light speed to run with the same constant speed.But man see light to follow a smaller destination,so for woman man's clock run slower,but for man woman's clock run slower too.
That is clear to me.

Good. And if it had been the woman shining the light at the man, the situation would have been reversed.

That what I want to ask is:"Both will count the same time at their clocks. For example If man counts 2 second,what about woman?"

No, you just answered that! "So for woman man's clock run slower,but for man woman's clock run slower too." The woman, if she could see the man's clock, would see that it had counted a shorter time than her clock. The man, if he could see the woman's clock, would see that it had counted a shorter time than his. That's the whole point of "relativity". Every observation is relative to the observer. The woman sees the man's clock running slower, the man sees the woman's clock running slower.

Sorry for my bad english.
Thanks a lot !

Don't worry about your English- it isn't perfect but it is understandable. My (put any language you choose here) is far worse!
In "so for woman man's clock run slower,but for man woman's clock run slower too" the precise English would have been "so for the woman the man's clock runs slower, but for the man the woman's clock runs slower too".
English is much stricter about "articles" than most languages. And the present tense, third person, of "run" is "runs". But you were 99% correct.

 

[Hepic]

Thank you a lot for everything. But I have one question too.
Lets say that Man counts 2 seconds,so man will think that woman's clock counted less than 2 seconds.
The same is for woman?? I mean,Woman counted 2 seconds,but will think that man's clock counted less than 2 seconds??

I am correct?

 

[Nugatory]

Thank you a lot for everything. But I have one question too.
Lets say that Man counts 2 seconds,so man will think that woman's clock counted less than 2 seconds.
The same is for woman?? I mean,Woman counted 2 seconds,but will think that man's clock counted less than 2 seconds??

I am correct?

If they are moving at a constant speed relative to one another, then yes, you are right.

The situation is symmetric; for both of them, they are at rest and the other one is moving relative to them, and the moving clock is running slow thanks to time dilation.

Because of relativity of simultaneity, there is no paradox here. As far as woman is concerned, at the same time that she marked the end of the second second, man's clock was marking the end of the first second. But as far as man is concerned, the moment when his clock marked off the end of the first second is not the same time that woman's clock marked off the end of the her second second.

 

[Hepic]

I have one question more now.
Lets say that man counts 10 years,so man if see at clock of woman will have pass 5 years for her.
That is the same for woman. She will count 10 years,but will when see at man's clock will see that for him have pass 5 years only.

I am correct?? If I am correct I will make my question.

 

[Nugatory]

I have one question more now.
Lets say that man counts 10 years,so man if see at clock of woman will have pass 5 years for her.
That is the same for woman. She will count 10 years,but will when see at man's clock will see that for him have pass 5 years only.

I am correct?? If I am correct I will make my question.

Is this not the same as your #4 above, except with years instead of seconds? If so, my answer in #5 still holds: "If they are moving at a constant speed relative to one another, then yes, you are right".

 

[Hepic]

Ok,perfect that what I mean.Lets say that man-woman are 20 years old. My question is:
If man counts 10 year for him(he will be 30 years old),and if for him woman's clock counted 5 years,woman for the man will be(25 years old).

That is the same from woman's point. She will see herself 30 years old,but man 25 years old.What happenes here??

 

[Nugatory]

Ok,perfect that what I mean.Lets say that man-woman are 20 years old. My question is:
If man counts 10 year for him(he will be 30 years old),and if for him woman's clock counted 5 years,woman for the man will be(25 years old).

That is the same from woman's point. She will see herself 30 years old,but man 25 years old.


What happenes here??

That's exactly what happens. Any time dependent process (the aging of the human body, sand falling through an hourglass, the decay of a sample of radioactive material, the motion of the Earth around its axis and around the sun, ...) can be used as a clock, and they are all equally affected by time dilation.

But there is still no paradox here; read what I said above about the relativity of simultaneity. Although in man's frame, his 30th birthday celebration is simultaneous with woman's 25th birthday celebration, but it does not follow that in woman's frame her 25th birthday celebration is simultaneous with his 30th birthday celebration.

To get a paradox, you would have to bring them together at the same location, so that we could compare their ages at the same time in the same frame. You can't do that if they're both moving at a constant speed relative to one another; and if you drop that assumption to bring them together, that's a different situation, the classic and much-discussed twin paradox.

 

[Hepic]

Yea,I see but if man look at the mirror he will see hisself to be old,but If woman see him via "phone",or something else the man be younger for her??
That is a bit strange :P

 

[Nugatory]

Yea,I see but if man look at the mirror he will see hisself to be old,but If woman see him via "phone",or something else the man be younger for her??
That is a bit strange :P

As long as they are at different locations and traveling at high speeds relative to one another, the image that reaches woman's phone (traveling no faster than the speed of light) will have left man long before he looked in the mirror... so it would be even stranger if he didn't look younger in woman's phone.

Now, if you had a way of transmitting an image instantaneously, then you could construct all sorts of horrible strange paradoxes. But there is no such thing.

 

[Hepic]

Thank you for your answers. Something final. Paradox of twins will happen only if spachip turns and come back again at earth. That gravitational force will make the man to think that woman's clock runs very fast.
I am correct?? If yes,why?

 

[Nugatory]

Thank you for your answers. Something final. Paradox of twins will happen only if spaceship turns and come back again at earth. That gravitational force will make the man to think that woman's clock runs very fast.
I am correct?? If yes,why?

Neither gravity nor acceleration are the explanation (although you will find many careless explanations that get this wrong). This is the "Twin Paradox", worth studying in its own right. There are many good threads in this forum, and a decent online overview at http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html

 

[Hepic]

Thank you a lot my friend.

 

[BruceW]

you can use 'gravity' to explain the twin paradox. i.e. in the traveling twin's 'reference frame' there will be a weird kind of 'gravity' which is due to the fact that this twin is undergoing accelerations. (note that I've used scare-quotes around the terms which are maybe not the proper terminology). But the problem is most easily explained by simply using an inertial reference frame.

edit: This was such a bad explanation, I'll give it another go. In the 'reference mollusc' (as Einstein called it) of the traveling twin, the metric is going to have terms due to the traveling twin accelerating around in the universe. These terms are essentially fictitious forces (a.k.a. 'gravity'). You can then calculate the time that passes according to the traveling twin and stay-at-home twin. And you can loosely say that this is due to 'gravity'. But then you can do all this in the inertial reference frame instead, which is much simpler, and the metric is simple.

edit again: I guess what I mean, is that if you want to see from both perspectives (the reference system of the stay-at-home twin and the reference system of the traveling twin) that everything works out the same and there is no paradox, then you can use 'gravity' to explain what happens in the perspective of the traveling twin.

 

[ghwellsjr]

Lets say that we have a spaship(with a man) that has speed,and a woman at ground that has not speed.

Lets say that man-woman are 20 years old. My question is:
If man counts 10 year for him(he will be 30 years old),and if for him woman's clock counted 5 years,woman for the man will be(25 years old).

That is the same from woman's point. She will see herself 30 years old,but man 25 years old.

What happenes here??

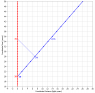
Let me illustrate with some spacetime diagrams. Since you described a scenario where the man and the woman are 20 years old when he takes off in a spaceship, I will first show a diagram depicting their mutual rest frame prior to launch and then the blue man takes off at 0.866c leaving the red woman behind. The dots represent 1-year intervals of time for both of them. We can call this the woman's rest frame:

So like you said, when she is 30 years old, he is 25 years old. I have included some more comparisons: when she is 40, he's 30 and when she's 50, he's 35. He accumulates age at one-half the rate she does in her rest frame.

Now let's look at a portion of the man's rest frame while he is traveling away from the woman:

Again, just like you said, when he's 30 years old, she is 25. Their ages are symmetrical when compared from their own rest frames.

Yea,I see but if man look at the mirror he will see hisself to be old,but If woman see him via "phone",or something else the man be younger for her??
That is a bit strange :P

I don't think it's strange if you see it on a spacetime diagram. Here is an example when the red woman sees the blue man via "phone" with a radio signal that traveled at the speed of light:

When she is 35 and he is 27.5 (in her rest frame), she can't actually see him at that age, rather, she will see him as he was at age 24, whether it's via "phone" or whether she is just looking at him via a suitable telescope. This is a 4 to 15 ratio.

Something final. Paradox of twins will happen only if spachip turns and come back again at earth. That gravitational force will make the man to think that woman's clock runs very fast.
I am correct?? If yes,why?

Although we don't have to explain this with gravity, you are correct that the man will observe (not just think) that the woman's clock runs very fast after he turns around. Just as the woman saw the man's clock running at 4/15 of her clock's rate, he sees her clock running slower than his by the same 4/15 ratio during the outbound portion of his trip. But as soon as he turns around, he starts seeing her clock running faster than his own by the inverse of the ratio, namely 15/4.

Here is a spacetime diagram of the entire trip in the rest frame of the woman indicating the signals going from the woman to the man showing that prior to his turn-around, he sees her clock running at 4/15 of his own and then after he turns around, he sees her clock running 15/4 of his own:

Now I want to show you a non-inertial diagram for the rest frame of the man during the entire scenario based on the radar method of determining the distance to the woman as a function of the man's own clock:

You can see that this diagram correctly depicts the signals traveling at c from the woman to the man and agreeing with all the observables in the inertial rest frame of the woman.

 

[hulberj]

I thought I had understood the difference in clock rate for different observers, but I am unable to answer the following problem:-
An observer O is stationary in an inertial frame of reference, with two stationary clocks which are some arbitrary distance apart.
A rocket ship flies through the IRF at high speed, brushing past each clock as it goes. Each clock records the time of the "fly past", so the observer O measures a time interval 'To' for the rocket to pass between his two clocks.
There is an astronaut A and a clock on board the rocket ship; this clock too records the time of each "fly past". So the astronaut A measures a time interval 'Ta' for the rocket to pass between the observer's two clocks..
The observer O sees the clock on the spaceship going at a slower rate than his own two clocks, but astronaut A sees O's clocks going more slowly than his own clock.
How do the two time intervals 'To' and 'Ta' compare with each other?
(Note that this is an extension of one of the standard thought experiments used to establish space contraction as seen by the speeding astronaut).

 

[BruceW]

yep. there is no contradiction with what you are saying. According to observer O, the clock held by astronaut A ticks slower than his own. And according to astronaut A, the clock held by observer O ticks slower than his own. Both statements are true. The important thing is that it is different when we use different reference frames. So you can only ask how time intervals T₀ and T_a compare with each other according to a specific reference frame. They will be different for different reference frames. So, for example, in a reference frame attached to the observer O, T₀ > T_a. But according to a reference frame attached to the astronaut A, T₀' < T_a' where the prime denotes that we are now talking about variables according to another reference system than before.

 

[ghwellsjr]

I thought I had understood the difference in clock rate for different observers, but I am unable to answer the following problem:-
An observer O is stationary in an inertial frame of reference, with two stationary clocks which are some arbitrary distance apart.

And, we will assume that observer O has previously synchronized those two clocks according to Einstein's convention, correct?

A rocket ship flies through the IRF at high speed, brushing past each clock as it goes. Each clock records the time of the "fly past", so the observer O measures a time interval 'To' for the rocket to pass between his two clocks.
There is an astronaut A and a clock on board the rocket ship; this clock too records the time of each "fly past". So the astronaut A measures a time interval 'Ta' for the rocket to pass between the observer's two clocks..
The observer O sees the clock on the spaceship going at a slower rate than his own two clocks, but astronaut A sees O's clocks going more slowly than his own clock.

This is not correct. As the astronaut is approaching observer O and his clocks, they all see the other ones clock going at a faster rate than their own, and to the same degree. Then, as the clocks pass and retreat from each other, they will see them going at a slower rate than their own, again, to the same degree.

How do the two time intervals 'To' and 'Ta' compare with each other?

'To' is always greater than 'Ta', assuming that the two clocks used to calculate 'To' have been synchronized in their mutual rest frame.

(Note that this is an extension of one of the standard thought experiments used to establish space contraction as seen by the speeding astronaut).

 

[ghwellsjr]

yep. there is no contradiction with what you are saying. According to observer O, the clock held by astronaut A ticks slower than his own. And according to astronaut A, the clock held by observer O ticks slower than his own. Both statements are true. The important thing is that it is different when we use different reference frames. So you can only ask how time intervals T₀ and T_a compare with each other according to a specific reference frame. They will be different for different reference frames.

I think you should read the scenario carefully and you will see that the question regarded the Proper Times displayed on inertial clocks, not the Coordinate Times of any reference frames. As such, it doesn't matter what reference frame is used, the measurements that are made are the same in all reference frames.

So, for example, in a reference frame attached to the observer O, T₀ > T_a. But according to a reference frame attached to the astronaut A, T₀' < T_a' where the prime denotes that we are now talking about variables according to another reference system than before.

Even if you are comparing the Proper Time interval between two events of one inertial clock to the Coordinate Time interval for those events, which can be different in different reference frames, the Proper Time interval will never be more than the Coordinate Time interval and they will be the same in the rest frame of the clock.

 

[yuiop]

I thought I had understood the difference in clock rate for different observers, but I am unable to answer the following problem:-
An observer O is stationary in an inertial frame of reference, with two stationary clocks which are some arbitrary distance apart.
A rocket ship flies through the IRF at high speed, brushing past each clock as it goes. Each clock records the time of the "fly past", so the observer O measures a time interval 'To' for the rocket to pass between his two clocks.
There is an astronaut A and a clock on board the rocket ship; this clock too records the time of each "fly past". So the astronaut A measures a time interval 'Ta' for the rocket to pass between the observer's two clocks..
The observer O sees the clock on the spaceship going at a slower rate than his own two clocks, but astronaut A sees O's clocks going more slowly than his own clock.
How do the two time intervals 'To' and 'Ta' compare with each other?
(Note that this is an extension of one of the standard thought experiments used to establish space contraction as seen by the speeding astronaut).

'To' will always be less than 'Ta' when there is a non zero spatial interval between the two events. As a general rule the time interval between two events that occur at the same location in a given inertial reference frame, will be less than the time interval between the same two events measured in any other IRF.

 

[ghwellsjr]

'To' will always be less than 'Ta' when there is a non zero spatial interval between the two events. As a general rule the time interval between two events that occur at the same location in a given inertial reference frame, will be less than the time interval between the same two events measured in any other IRF.

Your general rule is correct but you got 'To' and 'Ta' interchanged.

 

[yuiop]

Your general rule is correct but you got 'To' and 'Ta' interchanged.

Ah yes, I did. Well spotted.

 

[BruceW]

I was using T₀ and T_a as the time which passes on the observer O's clock and the time that passes on the astronaut A's clock (respectively), according to a reference frame attached to observer O. And I was using T₀' and T_a' as the time which passes on the observer O's clock and the time that passes on the astronaut A's clock (respectively), according to a reference frame attached to astronaut A. So I'm guessing my definitions are different to yours. My definitions are only referring to coordinate times. I make no mention of proper times.

In this definition, it is true that T₀ > T_a and T₀' < T_a'. hulberj was asking about why this is true (even though it looks paradoxical), but I was explaining it is true and is not a paradox in relativity.

 

[yuiop]

In this definition, it is true that T₀ > T_a and T₀' < T_a'. hulberj was asking about why this is true (even though it looks paradoxical), but I was explaining it is true and is not a paradox in relativity.

I think we are both correct in the context of our slightly different definitions. hulberj defined T₀ in terms of 2 spatially separated clocks which is a coordinate time interval and T_a in terms of a single clock at rest with respect to the astronaut, so T_a is effectively a proper time interval.

 

[ghwellsjr]

I was using T₀ and T_a as the time which passes on the observer O's clock and the time that passes on the astronaut A's clock (respectively), according to a reference frame attached to observer O. And I was using T₀' and T_a' as the time which passes on the observer O's clock and the time that passes on the astronaut A's clock (respectively), according to a reference frame attached to astronaut A. So I'm guessing my definitions are different to yours. My definitions are only referring to coordinate times. I make no mention of proper times.

Four times, you have used the expression, "the time which passes on the ... clock". That is the commonly accepted definition of Proper Time. If you're going to redefined terms, you should you explicitly state your definition, otherwise, confusion abounds.

Furthermore, if you mean something different than what hulberj meant, it's still unclear what you think those two time intervals refer to. Maybe you could explain.

In this definition, it is true that T₀ > T_a and T₀' < T_a'. hulberj was asking about why this is true (even though it looks paradoxical), but I was explaining it is true and is not a paradox in relativity.

Hulberj asked, "How do the two time intervals 'To' and 'Ta' compare with each other?" He didn't ask what you say he asked.

Furthermore, his statement that each observer sees the others clock running slower than his own is wrong as I pointed out in post #19.

Let's take a specific example to help understand what's going on here. Let's assume that the rocket ship with astronaut A (shown in black) is traveling at 0.6c with respect to observer O's rest frame and that one of observer O's clocks is colocated with him (shown in blue) and the other one (shown in red) is 3000 feet away. All clocks start out at zero in observer O's rest frame. Here is a spacetime diagram showing the "fly past" of the rocket ship past the two clocks. The dots represent 1-microsecond intervals of time on each clock. I'm defining the speed of light to be 1000 feet per microsecond:

The first thing to note here is that as the rocket ship is approaching observer O, observer O sees the astronaut's clock running at twice the rate of his own and then as it goes past observer O, he sees it running at one-half the rate of his own clock.

Then note the times on all three clocks at the two "fly pasts". The astronaut measures a time interval of 4 microseconds between the two "fly pasts" since his clock was at 4 for the first "fly past" and at 8 for the second "fly past". Observer O's first clock measured 5 at the first "fly past" and 10 at the second "fly past" so he calculates a time interval of 5 microseconds. So 'To' is greater than 'Ta' since 'To' equals 5 and 'Ta' equals 4.

Now I want to repeat the same spacetime diagram except with light signals to show how the black astronaut sees the blue observer's clock running at twice the rate of his own before the "fly past" and half the rate of his own after the "fly past":

Next I want to transform the events (the dots) from observer O's rest frame to the astronaut's rest frame and we will see that all the observations and measurement remain the same. First is the diagram showing what observer O sees of the astronaut's clock:

And finally the diagram that shows what the astronaut sees of observer O's clock:

I hope this clears up all confusion. Hulberj, does this make everything clear to you?

 

[BruceW]

I'm pretty sure that hulberj wanted to know why it is that according to each person, the clock of the other person ticks slower, and why this is not a paradox. I'm not taking into account the fact that the light from one person will take some time to travel between the two people. I'm saying what is the actual time that passes on the clock of the other person. i.e. if you are flying towards me, then according to me, your clock will be ticking slower than mine. I don't care about what each person sees. (If you like, you can assume that each person knows the rules of relativity, and can therefore calculate how fast the other person's clock is ticking, by seeing the light emitted by that clock).

In my definition, T_o T_a Are the coordinate times of the observer and astronaut in the observer's frame of reference. And T_o' T_a' are the coordinate times of the observer and astronaut in the astronaut's frame of reference.

So T_o is equal to the proper time which passes for the observer and T_a' is the proper time which passes for the astronaut. it's pretty standard notation to use a prime for the same coordinate according to a different reference frame, so I have done the definitions that way.

 

[ghwellsjr]

I'm pretty sure that hulberj wanted to know why it is that according to each person, the clock of the other person ticks slower, and why this is not a paradox. I'm not taking into account the fact that the light from one person will take some time to travel between the two people. I'm saying what is the actual time that passes on the clock of the other person. i.e. if you are flying towards me, then according to me, your clock will be ticking slower than mine. I don't care about what each person sees. (If you like, you can assume that each person knows the rules of relativity, and can therefore calculate how fast the other person's clock is ticking, by seeing the light emitted by that clock).

I think I'll wait until hulberj comes back and clearly states what he wanted to know if it wasn't what he already clearly asked about.

Yes, I would like you to describe precisely how each person can calculate how fast the other person's clock is ticking, by seeing the light emitted by that clock.

In my definition, T_o T_a Are the coordinate times of the observer and astronaut in the observer's frame of reference. And T_o' T_a' are the coordinate times of the observer and astronaut in the astronaut's frame of reference.

So T_o is equal to the proper time which passes for the observer and T_a' is the proper time which passes for the astronaut. it's pretty standard notation to use a prime for the same coordinate according to a different reference frame, so I have done the definitions that way.

Hulberj described two events which he called "fly pasts". The astronaut's clock was present at both those events. Therefore, it appears that you are associating Ta' with the Proper Time interval between those two events as measured by the astronaut's clock. In my example, this is 4 microseconds. And in the observer's rest frame, this has a coordinate time interval, which you call Ta, of 5 microseconds, agreed?

I'm assuming that when you say To is the Proper Time interval which passes for the observer, you are associating that with the coordinate time interval between the two events, correct? And even though hulberj specifically described this time interval as the difference between two readings on two different clocks that were each present at one of the events, you're describing this separately as the same interval on both clocks, correct? So in my example, if we take the clock colocated with the blue observer and look at it in the astronaut's rest frame, its time coordinate spans from 0 to 6.25 microseconds, correct?

So to summarize:

Ta' = 4
Ta = 5
To = 5
To' = 6.25

Did I do this right? If not, can you explain where I went wrong and fix whatever needs fixing?

 

[hulberj]

Thanks to everyone trying to sort out my confusion. Apologies if I have not used the accepted notation for the times.
Firstly about those clocks. I see them as recording clocks. The observer's two clocks are synchronised at the start. Every clock, when it observes an event, prominently displays its recorded time so that it can be read by the observer, the astronaut, (and by us!). (Is that the "proper time"?) I used the term "fly-past" to indicate that when the event occurred, the astronaut's clock and the observer's clock were both present in the same position in space.
Secondly, I am puzzled by the statement made by Ghwellsjr that:-
Quote: "The first thing to note here is that as the rocket ship is approaching observer O, observer O sees the astronaut's clock running at twice the rate of his own and then as it goes past observer O, he sees it running at one-half the rate of his own clock."
I thought that a clock in a moving frame will always be seen to be running slow, or "dilated". A classic example is the muon particle created in the Earth's upper atmosphere, which travels very fast but has an extremely short half-life. The muons seem to age more slowly according to an observer on the ground, and so that many more muons actually reach the ground than would be the case in a non-reletivistic environment.

 

[TumblingDice]

A clock moving relative to an inertial reference frame will always be calculated as ticking more slowly. That's different than how it is 'seen' where it's subject to a Doppler effect, so it's seen ticking faster when approaching and slower when receding.

 

[yuiop]

Firstly about those clocks. I see them as recording clocks. The observer's two clocks are synchronised at the start.

OK, let's say the observer's two clocks (A and B) are 1 light second apart in the the rest frame of the clocks and the observer. You need to be clear that they are synchronised only in this reference frame and in any other reference frame they will not appear to be synchronised.

Every clock, when it observes an event, prominently displays its recorded time so that it can be read by the observer, the astronaut, (and by us!). (Is that the "proper time"?)

The proper time is the normally the time indicated by a singe clock such as the clock of the astronaut. The astronaut's clock requires no synchronisation and does not require any calculations to obtain the elapsed time between the two events. The time measured b the observer is a calculated time using two clocks and this type of time interval is known as a coordinate time.

I used the term "fly-past" to indicate that when the event occurred, the astronaut's clock and the observer's clock were both present in the same position in space.

This is good practice. When the clocks are present at the same position we do not need to worry about how light travel times affect what is seen.

Secondly, I am puzzled by the statement made by Ghwellsjr that:-
Quote: "The first thing to note here is that as the rocket ship is approaching observer O, observer O sees the astronaut's clock running at twice the rate of his own and then as it goes past observer O, he sees it running at one-half the rate of his own clock."

Ghwellsjr is talking about what is actually "seen" when the clocks are in transit and this is affected by light travel times. When a clock approaches an observer, the gap between consecutive pulses appears to be shorter than the ticking rate of the clock because the clock is closer to the observer with each tick. This is known as the Doppler affect and occurs in Newtonian physics where all clocks are considered to run at the same rate. You can think of it as an optical illusion because the classic Doppler shift does not mean the clocks are actually running slower. In relativity, time dilation and Lorentz transformations allow for light travel time and remove any classic Doppler effects so that only the true time dilation is calculated.

I thought that a clock in a moving frame will always be seen to be running slow, or "dilated".

The word "seen" is used carelessly in relativity and can cause confusion. It is best to imagine collocated clocks that are next to each other when comparing times (as you did in your post). To continue with the example above, imagine the astronaut is traveling from A to B with a velocity of 0.8c. When the astronauts clock is next to clock A let's say both the astronaut's clock and the A clock read zero. On arrival at B, the B clock reads 1.25 seconds and the astronauts clock reads 0.75 seconds. According to the observer, the difference between his two clocks is greater than the time recorded on the astronaut's single clocks so he says the astronauts clock is ticking slower.

Now we look at things from the astronauts point of view. In his reference frame his clock and the A clock are both initially reading zero but the B clock reads L*v = 0.8 seconds. This is because the two clocks of the observer do not appear to be synchronised in the astronaut's reference frame. On arrival at B the astronauts that his clock reads 0.75 seconds and the B clock reads 1.25 seconds just as in the other reference frame, but according to the astronaut the B clock already has 0.8 seconds indicated at the start so the B clock has only advanced by (1.25-0.8 = 0.45) seconds. The astronaut concludes that the B clock is ticking slower than his own clock. The same is true when he compares notes with readings on the A clock.

Note that in either reference frame, the ticking rate of any clocks moving relative to the reference frame is slower than clocks at rest in the reference frame. Thus the observer and the astronaut calculate the other person's clocks to be running slower than their own. This is always true in Special Relativity but it also true that the elapsed proper time recorded by a single clock moving inertially between two events (such as the clock of the astronaut), will always be less than the coordinate time interval calculated from spatially separated clocks. The difference is subtle and you should do some calculations of your own or draw some spacetime diagrams to get your head around it. Closely studying the excellent spacetime drawings presented by Ghwellsjr would be a good place to start.

 

[ghwellsjr]

Thanks to everyone trying to sort out my confusion. Apologies if I have not used the accepted notation for the times.
Firstly about those clocks. I see them as recording clocks.

Yes, you made that very clear in your first post.

The observer's two clocks are synchronised at the start.

Even though you didn't make this clear, I assumed that you meant them to be synchronized.

Every clock, when it observes an event, prominently displays its recorded time so that it can be read by the observer, the astronaut, (and by us!). (Is that the "proper time"?)

Yes, every clock always displays its own Proper Time.

I used the term "fly-past" to indicate that when the event occurred, the astronaut's clock and the observer's clock were both present in the same position in space.

Yes, you also made that very clear.

Secondly, I am puzzled by the statement made by Ghwellsjr that:-
Quote: "The first thing to note here is that as the rocket ship is approaching observer O, observer O sees the astronaut's clock running at twice the rate of his own and then as it goes past observer O, he sees it running at one-half the rate of his own clock."
I thought that a clock in a moving frame will always be seen to be running slow, or "dilated". A classic example is the muon particle created in the Earth's upper atmosphere, which travels very fast but has an extremely short half-life. The muons seem to age more slowly according to an observer on the ground, and so that many more muons actually reach the ground than would be the case in a non-reletivistic environment.

You can't see a clock running at the determined Time Dilation rate, you see it at the Doppler rate. Even in the case of muons, in the Earth's rest frame, we don't see their creation at the time it happens, we see it ever so slightly before we see the muon's arrival. So from creation to arrival is a very small fraction of a microsecond, even if the muon lasted for 2 microseconds in its rest frame and almost 45 microseconds in Earth's rest frame, assuming a speed is 0.999c. Here's a spacetime diagram for the blue Earth's rest frame showing the muon in red:

It's impossible to see in this drawing but there are two red lines showing how Earth views the creation of the muon and how it views it at 1 microsecond later, so I have zoomed in on the end of the life of the muon where we on the Earth can see its creation and half-way through its life:

In effect, we see the muon's "clock" ticking at 44.7 times faster (the Doppler factor) than the rate of our own clock, not 22.4 times slower (the Time Dilation factor). Note that the Time Dilation factor is clearly visible on the first spacetime diagram since the 1-microsecond tick marks for the muon are spaced out to 22.4 times according to the Coordinate Time. If you want, I can show you how the Time Dilation can be determined by Earth observers for their rest frame in the muon scenario or in your scenario. And keep in mind that in other frames, the propagation time for the signals can change but what the observers actually see remains the same.

Aside from the Doppler puzzle, were the diagrams clear or did you have any more questions regarding them?