Closest approach of two trains on perpendicular tracks

[stunner5000pt]

Kinda confused on this one becuase of the time difference involved

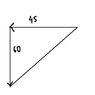
A train leaves a station going south at 60 km/hr at 10:00. Another train heading due west reaches this station at 11:00. The latter train was traveling at 45km/hr. At what time are they the closest?

To start with the 45 train is 45km away from teh station and in the end the distnace is 60 km
iformulated something like 45(1-t) + 60t = Distance
but that doesn't yield the answer i need...
can someone help!

 

[chroot]

Call the point at which the 60 km/hr train starts the "origin." You know the direction and distance of each train from the origin at any given time.

As shown in your figure, the vectors from the origin to each train form a right triangle, the hypotenuse of which is the distance between them.

If you know the length of the triangle's legs as a function of time, use the Pythagorean formula to find the length of the triangle's hypotenuse as a function of time. Then, find the minimum of that function.

- Warren

 

[thepatientmental]

Based on the given information, we can use the distance formula d = rt to determine the distance of each train from the station at any given time. Let's use t as the time in hours since 10:00. For the train heading south, its distance from the station can be represented as d = 60t. For the train heading west, its distance from the station can be represented as d = 45(1-t). We can set these two equations equal to each other to find the time when they are closest to each other:

60t = 45(1-t)
60t = 45 - 45t
105t = 45
t = 45/105
t = 0.43 hours

Therefore, at 10:26 (10:00 + 0.43 hours), the trains will be closest to each other. This is because at this time, the southbound train will be 25.8 km away from the station, while the westbound train will be 19.4 km away. This is the minimum distance that they will be from each other during their journey. I hope this helps clarify the situation.