Collision between two bodies with same mass

[DarkFalz]

Hello, its my first time in this forum, I've registered because sometimes i have some physics questions during my free times (maybe not the best free time "sports" xD).

The question is the following, according to the linear momentum conservation with elastic bodies, when a mass m1 with velocity v1 collides with a mass m2 which was stationary, mass m1 will become stationary and m2 will move with velocity v1.

The problem is that i just can't understand what is happening during the collision, from my naive point of view, when m1 collides with m2, it exerts a force on m2 because m2 is in m1 path, as such m1 will transfer is velocity to m2.

The problem is that I've heard that not just one force is exerted between the two bodies, and that the forces vary according to the following function:

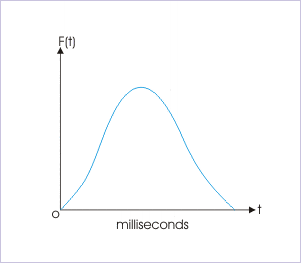
That makes me wonder the following, in the beginning of the collision, let's say, until the maximum of the function, the mass m1 loses half its speed, and m2 gains half m1 speed, since half the total force has been exerted between the two bodies. if that's the case, at that point both bodies will have the same speed and won't be in contact anymore, so the collision would stop. What am i missing here? Where am i thinking wrong?

Thanks in advance

 

[xts]

the mass m1 loses half its speed, and m2 gains half m1 speed, since half the total force has been exerted between the two bodies. if that's the case, at that point both bodies will have the same speed and won't be in contact anymore, so the collision would stop. What am i missing here? Where am i thinking wrong?

Why do you think they won't be in contact anymore?
My advice: go to the siding rail and see the collisions (watch bumpers!) between cars, as they are re-aranged

 

[chrisbaird]

First of all, m1 will only end up stationary in the end if m1 = m2.

If the masses are perfectly rigid and the collision is perfectly elastic (which is what it sounds like you have in mind), your curve would have to be made infinitely thin and infinitely tall in such away that its integral is still the total force. Then your problems of them not being in contact anymore goes away.

The finite curve you posted is more realistic. It is the curve for two masses colliding that are deforming as they collide. In that case, they are in contact the whole time the force is exerted and this is made possible despite their different speeds because they are deforming properly to stay in contact.

In the picture below, you can tell that both objects involved in the collision are deforming upon impact so that they are in contact for the whole interaction despite being at different (and continually changing) speeds during the interactionhttp://www.popular-pics.com/PPImages/Deep-Impact-football.jpg .

 

[DarkFalz]

Oh, i understand now, since they compress, they remain in contact even after half the force has been transfered, with the decompression phase allowing for the rest of the force to be applied. Is that it?

 

[xts]

Exactly!

 

[DarkFalz]

Ok, i understand now, thanks a lot xD