DarkFalz
- 71
- 0
Hello, its my first time in this forum, I've registered because sometimes i have some physics questions during my free times (maybe not the best free time "sports" xD).
The question is the following, according to the linear momentum conservation with elastic bodies, when a mass m1 with velocity v1 collides with a mass m2 which was stationary, mass m1 will become stationary and m2 will move with velocity v1.
The problem is that i just can't understand what is happening during the collision, from my naive point of view, when m1 collides with m2, it exerts a force on m2 because m2 is in m1 path, as such m1 will transfer is velocity to m2.
The problem is that I've heard that not just one force is exerted between the two bodies, and that the forces vary according to the following function:
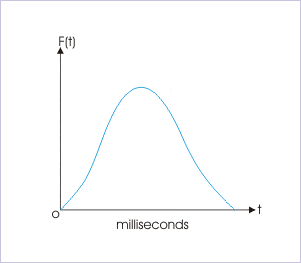
That makes me wonder the following, in the beginning of the collision, let's say, until the maximum of the function, the mass m1 loses half its speed, and m2 gains half m1 speed, since half the total force has been exerted between the two bodies. if that's the case, at that point both bodies will have the same speed and won't be in contact anymore, so the collision would stop. What am i missing here? Where am i thinking wrong?
Thanks in advance
The question is the following, according to the linear momentum conservation with elastic bodies, when a mass m1 with velocity v1 collides with a mass m2 which was stationary, mass m1 will become stationary and m2 will move with velocity v1.
The problem is that i just can't understand what is happening during the collision, from my naive point of view, when m1 collides with m2, it exerts a force on m2 because m2 is in m1 path, as such m1 will transfer is velocity to m2.
The problem is that I've heard that not just one force is exerted between the two bodies, and that the forces vary according to the following function:
That makes me wonder the following, in the beginning of the collision, let's say, until the maximum of the function, the mass m1 loses half its speed, and m2 gains half m1 speed, since half the total force has been exerted between the two bodies. if that's the case, at that point both bodies will have the same speed and won't be in contact anymore, so the collision would stop. What am i missing here? Where am i thinking wrong?
Thanks in advance