JSGandora
- 92
- 0
Yellow light shines on a sheet of paper containing a red pigment. We want to determine the color that we see. The obvious solution is this:
Yellow can be though of as green and red light. Thus, green and red light can be though of striking the paper with red pigment. Red pigment absorbs its complementary color, which is cyan which can also be though of as blue and green. Thus, we are basically reduced to this problem:
Green and red light strikes paper that absorbs blue and green light. Thus, only red light is reflected and thus the paper appears red.
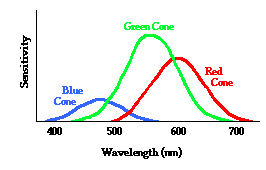
However, as far as I know, this is just a convention to simplify the subtractive color mixing process. However, the pigment only absorbs the frequency of cyan because the electrons vibrate to that frequency. I'd think that cyan can't be split to absorb two different frequencies instead of one. We only use this convention because our three kinds of cones on our retina overlap in receiving different wavelengths of light so that receiving red and green light is no different than receiving yellow light. So how can this be applied to pigments with flaw?
Yellow can be though of as green and red light. Thus, green and red light can be though of striking the paper with red pigment. Red pigment absorbs its complementary color, which is cyan which can also be though of as blue and green. Thus, we are basically reduced to this problem:
Green and red light strikes paper that absorbs blue and green light. Thus, only red light is reflected and thus the paper appears red.
However, as far as I know, this is just a convention to simplify the subtractive color mixing process. However, the pigment only absorbs the frequency of cyan because the electrons vibrate to that frequency. I'd think that cyan can't be split to absorb two different frequencies instead of one. We only use this convention because our three kinds of cones on our retina overlap in receiving different wavelengths of light so that receiving red and green light is no different than receiving yellow light. So how can this be applied to pigments with flaw?