lalapnt
- 17
- 0
how do i work this out?
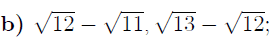
I like this approach. You can see at a glance which difference is larger.tahayassen said:Think of the square root function graphed.
tahayassen said:Think of the square root function graphed.
arildno said:Remember that for any two numbers, a and b, we have: (a-b)*(a+b)=a^2-b^2
i don't want to solve this graphically. (not like i even know how. I need some help here)tahayassen said:Think of the square root function graphed.
Are you saying you don't know what the graph of y = ##\sqrt{x}## looks like?lalapnt said:i don't want to solve this graphically. (not like i even know how. I need some help here)
Mark44 said:Are you saying you don't know what the graph of y = ##\sqrt{x}## looks like?
The graph of y = √x is one of the first ones you learn when you learn to graph functions. If you are asking questions about square roots, it's one you should know.lalapnt said:oh no! i know that! but first, i don't want to solve this graphically even if i did, how does the graph of y = √x help out?
EDIT: if i knew everything in math, i wouldn't be here.
Mark44 said:The graph of y = √x is one of the first ones you learn when you learn to graph functions. If you are asking questions about square roots, it's one you should know.
Look at the graph of this function. Does the y value on the graph change more between 11 and 12 than it does between 12 and 13, or does it change less between 11 and 12 than it does between 12 and 13?
but how is 2sqrt(12) = 48? :/dextercioby said:Purely algebra ?
Place ? i/o =, > or <.
sqrt(12)-sqrt(11) ? sqrt(13)-sqrt(12)
2sqrt(12) ? sqrt(11)+sqrt(13)
48 ? ...
Can you continue ?
Mark44 said:I doubt that any instructor would accept a proof in which most of the symbols are ?.
piercebeatz said:You could make it an equation and use the same method... i.e. let root(13)-root(12)+x=root(12)-root(11). If x>0, then the left side is greater. If x<0, the right side is greater
micromass said:If the left side is greater, then you can't write an = between the sides.
Am I understanding you wrong?
And then the problem becomes determining the sign of x.piercebeatz said:You could make it an equation and use the same method... i.e. let root(13)-root(12)+x=root(12)-root(11). If x>0, then the left side is greater. If x<0, the right side is greater
Mark44 said:And then the problem becomes determining the sign of x.