TryingTo
- 6
- 0
Hi all,
I study binding of analytes in a platform where I have 10.000 sensors. there's is one binding event per sensor and I identify it as a sudden positive change in the signal. I do first a control experiment without analytes. I measure the maximum change in the signal for each sensor and I obtain a narrow gaussian distribution around cero due to electric noise (green curve). When I measure the analytes I obtain a kind of Gumbel distribution because some sensors detect a positive binding event (larger than the electronic noise, red curve). When I compare the histograms is clear that there is a difference before and after but I would like to do a quantitative analysis of how different the distributions are. Do you have any clue on how to do this? Which test I could apply? One of the distributions is normal but the other is not so I'm not sure.
Thank you!
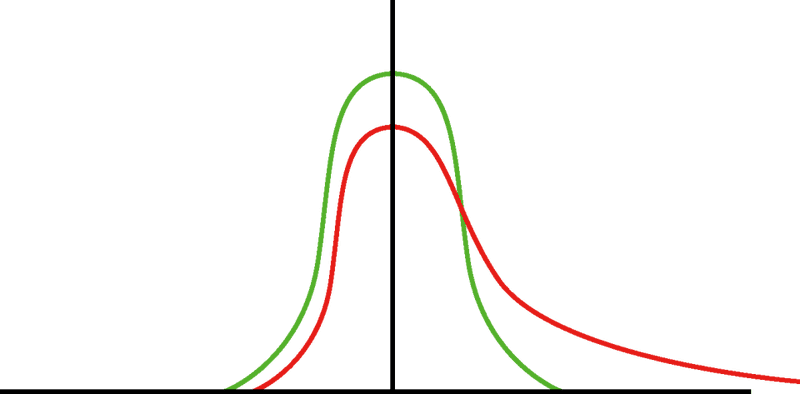
I study binding of analytes in a platform where I have 10.000 sensors. there's is one binding event per sensor and I identify it as a sudden positive change in the signal. I do first a control experiment without analytes. I measure the maximum change in the signal for each sensor and I obtain a narrow gaussian distribution around cero due to electric noise (green curve). When I measure the analytes I obtain a kind of Gumbel distribution because some sensors detect a positive binding event (larger than the electronic noise, red curve). When I compare the histograms is clear that there is a difference before and after but I would like to do a quantitative analysis of how different the distributions are. Do you have any clue on how to do this? Which test I could apply? One of the distributions is normal but the other is not so I'm not sure.
Thank you!