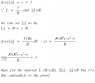Complex Analysis Radius of Convergence.

[kidsasd987]

Hello, I have two questions regarding the Radius of convergence.

1. What should we do at the interval (R-eps, R)
2. It used definition to prove radius of convergence, but I am not sure if it is necessary-sufficient condition of convergence. I get that this can be a sufficient condition but not sure of the necessity

 

[FactChecker]

If I understand the question, this may help -- The ε was picked arbitrarily small so the proof shows convergence all the way to ε = 0. So there really is no specific interval (R-ε, R) to worry about.

 

[kidsasd987]

what I am concerend about is,

hm the author used (L+eps)|Z|<1 to argue that L^n*|Z|^n < (L+eps)^n|Z|^n < r^n whereas r<1

but the thing is as I showed at the uploaded png file (if the derivation is correct), it is clear that |Z|= R-eps satisfies the condition |Z| < R and if |Z|= R-eps, r = 1.

which implies (L+eps)|Z|<1 cannot be true. for all |Z|<R
Ah, also I made a mistake. It should be R+R^2*eps-eps-R*eps^2
hmm do you agree?

 

[kidsasd987]

If I understand the question, this may help -- The ε was picked arbitrarily small so the proof shows convergence all the way to ε = 0. So there really is no specific interval (R-ε, R) to worry about.

maybe I screwed up at somewhere.

 

[FactChecker]

maybe I screwed up at somewhere.

Maybe not. But the point is that ε >0 is arbitrarily small (or r is arbitrarily near 1) so the the interval you are worried about shrinks down to nothing.

 

[kidsasd987]

Maybe not. But the point is that ε >0 is arbitrarily small (or r is arbitrarily near 1) so the the interval you are worried about shrinks down to nothing.

Although we ignore the interval, the argument that (L+eps)|Z|<1 does not hold true if we take |Z| = R - eps. (I guess) It just bugs me and I am stuck at that page ;(

and my last conclusion R<1 doesn't seem right at all too.

 

[Stephen Tashi]

It isn't clear to me what is to be proven. We've only been shown the last part of the text that states "the theorem".

 

[kidsasd987]

It isn't clear to me what is to be proven. We've only been shown the last part of the text that states "the theorem".

I am sorry.