Components of force of 2 moving charges

[pondzo]

Homework Statement

A particle with charge $e$ and position vector $\vec{r}$ (relative to some frame, S) moves with constant velocity $\vec{v}$. A second charge $e'$ is moving with the same velocity $\vec{v}$ through the field generated by $e$. If $\vec{d}$ is a vector from $e$ to $e'$ find the components of the force on $e'$ parallel to and normal to $\vec{d}$.

Homework Equations

We can assume the velocities involved are far less than the speed of light, thus:

$\vec{B}=\frac{\mu_0 e}{4\pi}\frac{\vec{v}\times\vec{r}}{r^3}$.

The Attempt at a Solution

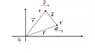
This is a previous exam question and the above equation is all that is given. So I'm not sure whether they would like us to calculate the magnetic and electric contributions to the force or just the magnetic. Also I am assuming that they mean the second charge is moving with velocity $\vec{v}$ relative to the first charge. This is how I imagine the geometry of the situation:

The velocity of $e'$ with respect to $e$ is: $\vec{v}_{e'e}=\dot{\vec{d}}=\dot{\vec{r}'}-\dot{\vec{r}}=2\vec{v}-\vec{v}=\vec{v}$
The magnetic field of $e$ in the rest frame of $e'$ is: $\vec{B}_{ee'}=\frac{\mu_0 e}{4\pi}\frac{\vec{(-v)}\times\vec{d}}{d^3}$. Or do I use the magnetic field of $e$ in the frame S?
Thus the force on $e'$ due to the magnetic field of $e$ is $\vec{F}_{mag}=\frac{e'e\mu_0}{4\pi}\vec{v}_{e'e}\times\frac{\vec{(-v)}\times\vec{d}}{d^3}$. But $\vec{v}_{e'e}$ is parallel to $\vec{v}$ so the cross product is zero. I must be thinking about the situation wrong since there should be a non-zero force.

Also, when I do eventually find the force, do I find the normal and parallel components by taking the scalar product of the total force with the normal and parallel vectors?

 

[tommyxu3]

Why do you think it the force should be zero? Many effects would be against our intuition, that at least in this case I think the theory doesn't tell us like this.