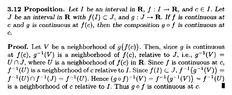Composition of Two Continuous Functions .... Browder, Proposition 3.12 .... ....

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...

I need some help in understanding the proof of Proposition 3.12 ...Proposition 3.12 and its proof read as follows:

View attachment 9519
In the above proof by Browder we read the following:

" ... ... Since $$f(I) \subset J$$, $$f^{ -1 } ( g^{ -1 }(V) ) = f^{ -1 } (U) \cap f^{ -1 } (J) = f^{ -1 } (U)$$ ... ... "My question is as follows:

Can someone please explain exactly why/how $$f^{ -1 } (U) \cap f^{ -1 } (J) = f^{ -1 } (U)$$ ... ...
Help will be much appreciated ...

Peter

 

[Jhoneine]

.The reason why f^{ -1 } (U) \cap f^{ -1 } (J) = f^{ -1 } (U) is because the inverse of a function is a one-to-one mapping, meaning that the same value can only map to one other value. Since J is a subset of I, any element in U will necessarily be in J, and thus the intersection of f^{ -1 } (U) and f^{ -1 } (J) will be f^{ -1 }(U).

 

[soloenergy]

Hi Peter,

I can try to help you understand this proof. First, let's define some notation. In this proof, f is a function mapping from interval I to interval J, and g is a function mapping from interval J to some other set V. U is a subset of J, and V is a subset of some other set W. The notation f^{-1}(U) means the set of all points in I that map to U under the function f.

Now, in the proof, we are trying to show that f^{-1}(g^{-1}(V)) = f^{-1}(U). In other words, we want to show that the set of points in I that map to V under the composition of functions g and f is the same as the set of points in I that map to U under f alone.

To do this, we first note that since f(I) is a subset of J, we can say that f^{-1}(J) is a subset of I. This means that any point in I that maps to J under f must also be in I itself. Now, since we know that f^{-1}(U) is a subset of I (since U is a subset of J), we can say that f^{-1}(U) intersect f^{-1}(J) must also be a subset of I. In other words, any point in I that maps to both U and J under f must also be in I itself.

This is where the key step comes in. Since f^{-1}(U) intersect f^{-1}(J) is a subset of I, we can say that it is also a subset of f^{-1}(U). In other words, any point in I that maps to both U and J under f must also map to U alone under f. This is why f^{-1}(U) intersect f^{-1}(J) = f^{-1}(U).

I hope this helps clarify the proof for you. Let me know if you have any other questions. Happy reading!