Compound Interest Paid in 3.5 Years: Regional Laws & Concepts

[SafiBTA]

- This may be a stupid question as I am totally new to the concept of interest. I don't even know if my question is valid.
- Figure is given below for referenceSuppose I deposit some money in a bank that pays compound interest on yearly basis. If I decide to withdraw my amount at the end of 3.5 years, which of the following amounts will the bank pay me back:

a. the amount accumulated at the end of 3 years ($450, as represented by blue plot)

b. the amount accumulated at the end of 3 years + a simple interest on this amount computed over 6 months
($560, as represented by the black plot; since compound interest is essentially the simple interest on the last accumulated amount)

c. the amount accumulated at the end of 3.5 years ($540, represented by red plot)

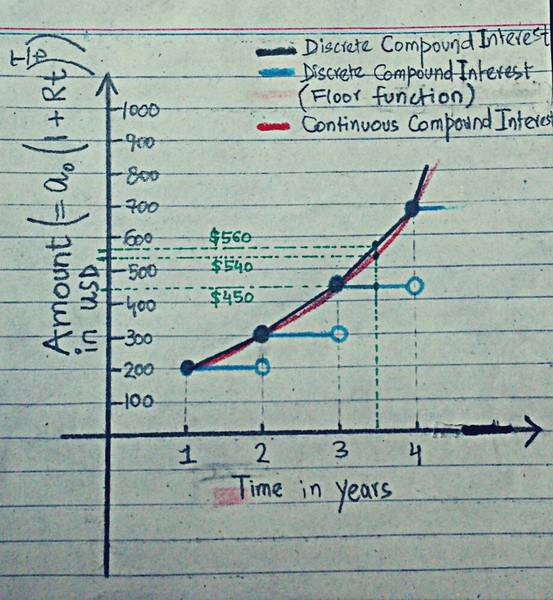
As far as I can think, it can't be c since the interest is compounded discretely and not continuously.

How is this problem usually tackled?

It looks like the amount depends upon the regional laws, but I just want to clarify my concepts.

 

[mfb]

That depends on the contract you signed.

There is also
(d) $450, but you can get $90 more at the end of the year (where do you get that crazy interest rate? :p)

 

[Dale]

Annually compounded interest would be a. The black line never happens in my experience, and the red line never intersects the blue.

 

[pwsnafu]

In the actuary exams (specifically CT1 in UK and FM2 in US) the answer is always $a_0 (1+i)^{3.5}$. Simple interest is only ever used if the total time is less than a year (eg zero coupon bonds maturing in 4 months). There's a couple of reason for this, but the main one is that actuaries are interested in very long time frames, such as 50 years, so the error is proportionally small. Second, they assume "consistent markets" which means the accumulations can be multiplied with each other.

At the other extreme traders are interested in weekly or even daily returns, so they'll immediately take money out of an annually compounded account, into something which pays fortnightly or weekly, even if that means a lower effective interest over the year. It's the price you pay for flexibility.

In reality, it would be dependent on the contract.
Also, if such bank existed switch banks! The standard in real life is monthly compounding, not annual.

 

[Locrian]

In the actuary exams (specifically CT1 in UK and FM2 in US) the answer is always $a_0 (1+i)^{3.5}$.

I do not think that is true, and think that it is a dangerous assumption to use on exam FM. It's entirely possible that a question would be asked where interest is only calculated once a year, resulting in his answer A (taking to the third power).

 

[pwsnafu]

I do not think that is true, and think that it is a dangerous assumption to use on exam FM. It's entirely possible that a question would be asked where interest is only calculated once a year, resulting in his answer A (taking to the third power).

The default assumption is consistent markets, that is the accumulation factors $A(t_1, t_2) \times A(t_2, t_3) = A(t_1, t_3)$ for any $t_1 < t_2 < t_3$. In order to work with force of mortality actuaries need to covert interest rates into the force of interest, which only works under this assumption.

Answer A is correct if the problem explicitly states not to assume consistency.

Edit: gets out lecture notes (my exams necessarily followed CT exams because they gave exemptions to them)

It might be thought that in view of transaction costs and taxes, a consistent markets is an unrealistic assumption. However, many (if not most) calculations and models involve rates of return achieved over periods when the closing valuation for one time interval becomes the opening valuation for the next time interval and no transactions actually take place. Also, except for real property, transaction costs are relatively insignificant for financial institutions. Consequently, consistent markets will be assumed, unless stated otherwise.

When the force of interest is constant, we re-define the compound interest functions $i$ and $v$ in terms of $\delta$. This makes it valid, in consistent markets, to use expressions such as $(1+i)^t$ and $v^t$ for non-integer values of $t$.
...
Also the accumulation factor $A(0,n) = exp\{ \int_0^n \delta ds \} = e^{n \times \delta}$ does not depend on $n$ being an integer. Hence it is valid, having defined $i$ in this fashion, to use the expressions
$(1+i)^t, v^t$ and $\left(1+\frac{i^{(p)}}{p} \right)^t$
when $t$ is not an integer

 

[Locrian]

When I took FM, they did not have to state that markets weren't consistent to set unusual intervals for interest to be calculated. I don't think this has changed, but I'll double check with a friend who took it recently to verify.

In order to work with force of mortality actuaries need to covert interest rates into the force of interest, which only works under this assumption.

Sure, but you don't usually have to work with force of mortality. I've worked with long timeline calculations that included both interest and mortality, and never used force of mortality or force of interest. I think it's actually pretty rare to do so in actual practice, though it may depend on what area you're in.

 

[pwsnafu]

When I took FM, they did not have to state that markets weren't consistent to set unusual intervals for interest to be calculated. I don't think this has changed, but I'll double check with a friend who took it recently to verify.

Interesting. I wonder if that's a difference between US and UK?

Edit: I just read the April CT1 exam and they had this question

3 £900 accumulates to £925 in four months.
Calculate the following:
(i) the nominal rate of interest per annum convertible half-yearly [2]
(ii) the nominal rate of discount per annum convertible quarterly [2]
(iii) the simple rate of interest per annum [2]
[Total 6]

To me that only makes sense under consistent. But they don't state it anywhere. So I'm sticking with what I said: assume consistent unless specifically asked otherwise.