Finance - Find Monthly Payments (two methods)

[jgiannis]

Hi.

I am looking into buying a home. I am trying to calculate the monthly "Principal + Interest." My bank actually provides a neat calculator that removes all of the guesswork (https://www.schoolsfirstfcu.org/wps/portal/Calculator?calculatorParamKey=MortgageCompare).

However, for the fun of math, I tried reaching the same value by using logic in my equation. But it turns out that my equation comes out different than the result from the bank's calculator.

Can anyone explain where my logical approach goes wrong?

Given the following information, here's how I ran the equation, from scratch, using logic:

Total Price of Home: $350,000
Down Payment (20%): $70,000
Principal Loan Amount to be Financed: $280,000
Interest Rate (APR-FIXED): 3.5%
Duration of Loan: 30 years
Frequency of Payment (monthly): 12

Thus, I figure that if I'm paying 3.5% per year on $280k, then every year I would be paying this much in interest: ($280k)*(0.035) = $9,800.

Thus, in 30 years, the total amount of interest that I would pay is: ($9,800)*(30) = $294,000.

Thus, the total amount of Principal + Interest that I would pay after 30 years would be: ($280,000)+($294,000) = $574,000

Thus, since there are 360 months in 30 years, the monthly cost of Principal + Interest would be: ($574,000)/(360) = $1,594.44.

However, using those same numbers, my bank's calculator says that the Principal + Interest would actually be $1,257.33.

I should note that I trust my bank's numbers. I found a finance equation online, and using that equation, I get the same result as my bank. However, the things that puzzle me so much are (a) where did my logical approach go wrong, and (b) what is the logic behind the "correct" financial equation? To me, the "correct" financial equation makes no sense. I do not see the logic in it. Here is the equation that I'm speaking of:

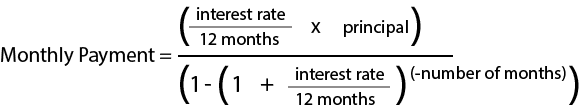
Also, to make things a bit more complicated, I was helping someone calculate a monthly car loan. Here's the given information:

Total Price of Car: $21,000
Down Payment: $7,000
Principal Loan Amount to be Financed: $14,000
Interest Rate (APR-FIXED): 9%
Duration of Loan: 5 years
Frequency of Payment (monthly): 12

I used the equation above, and I get a value of $290.62. Sounds good.

I also used my own logical approach, and I get a value of $338.33. Also sounds good, but based on the above home loan discussion, I assume this is wrong.

The thing that puzzles me this time around is that the car dealership quoted us $338.33. It sounds like they used the same approach as I initially thought of. Why? Is there typically a different calculation in Home Loans vs Car Loans? Thanks for your time.

 

[mfb]

The $280,000 go down over time, as some part of the $1,257.33 are used to reduce the debts you have. That means interest goes down as well.

If the car dealer asks for $338.33 they try to rip you off.

 

[jim mcnamara]

As you pay off principal, interest paid goes down, and payments applied to principal go up. And every time (360 payments) you make a payment, the payment gets applied to both principal and interest. But those amounts applied are different each time. In year one, very little is applied to principal. In year 30 almost all of the payment goes to principal.