gfd43tg
Gold Member
- 947
- 48
Hello,
I am simulating an experiment I did in the lab where we had air flow over a tray of water to determine the mass transfer coefficient scaling with velocity, as well as boundary layer thickness scaling with velocity.
Now I am using COMSOL to simulate the experiment, and here is the schematic set up
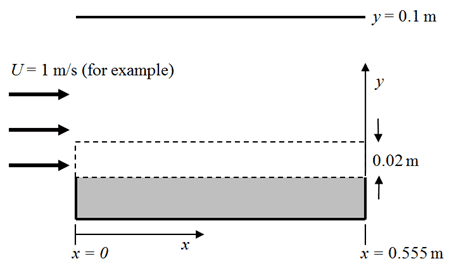
Where the dashed lines represents the control volume of the COMSOL simulation. I input my boundary conditions and here is what the concentration profile looks like
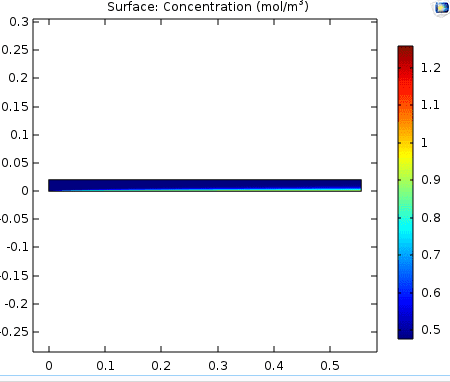
The blue area is the bulk air flow concentration, so it is clear that the teal area is the concentration boundary layer. Notice that the boundary layer gets thicker as you move more down the length of the tray. Why is this happening theoretically? I know it has something to do with the Blasius boundary layer.
Also, if anyone understands COMSOL or has any ideas how I could devise a way to figure out the boundary layer thickness as a function of position, that would be very helpful! I can plot the concentration gradient as a function of distance, so that might be a place to start to find the thickness.
Thanks
I am simulating an experiment I did in the lab where we had air flow over a tray of water to determine the mass transfer coefficient scaling with velocity, as well as boundary layer thickness scaling with velocity.
Now I am using COMSOL to simulate the experiment, and here is the schematic set up
Where the dashed lines represents the control volume of the COMSOL simulation. I input my boundary conditions and here is what the concentration profile looks like
The blue area is the bulk air flow concentration, so it is clear that the teal area is the concentration boundary layer. Notice that the boundary layer gets thicker as you move more down the length of the tray. Why is this happening theoretically? I know it has something to do with the Blasius boundary layer.
Also, if anyone understands COMSOL or has any ideas how I could devise a way to figure out the boundary layer thickness as a function of position, that would be very helpful! I can plot the concentration gradient as a function of distance, so that might be a place to start to find the thickness.
Thanks
Last edited: