Confusion about factoring in quantum computation

[Haorong Wu]

TL;DR Summary

Confusion about factoring in quantum computation

Hi, I'm currently learning QC with Nielsen's QCQI.

I've written a program in Matlab following the factoring algorithm in page 233 and 235.

I run the program for factoring 15, 18, and 25. I got the proper results several times, but I also got error reports sometime, especially when factoring 18 and 25.

After I checked the variables, I found that the probability distributions of the first register after $FT^+$ are spread. Well, I don't know how to describe it clear. Maybe I should put the data in the post:

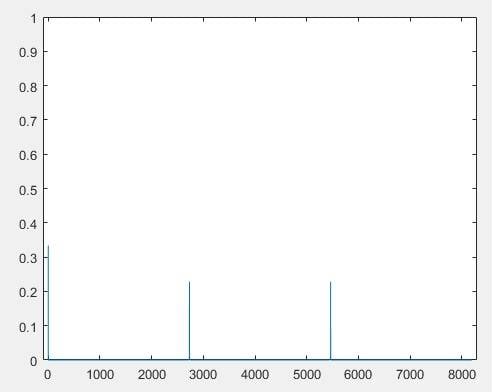
First, it seems that there are just three results with considerable probabilities.

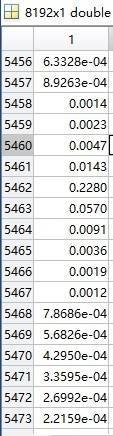
However, as we can see, the data from 5457 to 5466 are all big enough that anyone of them can be a result for a measurement.

And, in the algorithm, the next step would be computing $r$ from $\frac s r$. For example, I got a measurement result of 5461, then from $\frac {5461} {8192}$, the $r$ would just be 8192. Then $gcd \left( N,x^{r/2}+1 \right)$ would report error, where $N=18, x=7$. I believe this is because the $r$ is too large to compute the greatest common divisor.

Then, if a measurement really gave me a result of 5461, how should I use the continued fraction expansion to get the proper order $r$? I can't understand what role does the continued fraction expansion play.

Thanks for any suggestions.

 

[tnich]

The continued fraction expansion is a way of finding a rational number close to a phase estimate produced in the order-finding algorithm. Since that algorithm operates on $t$ qubits, it only produces an approximation of the phase $\tilde \phi$. If you work through the continued fraction algorithm with $\tilde {s / r} = \frac {5461}{8192}$. You get successive rational numbers 0,1, $\frac 1 2$, $\frac 2 3$, $\frac {5461}{8192}$. So the closest rational number to $\tilde \phi$ other than $\frac {5461}{8192}$ itself is $\frac 2 3$, making $r=3$. In fact $7^3 = 1 \text{ mod } 18$, so it is the correct value for $r$. Unfortunately, it is not an even number, so it won't work for the rest of the algorithm. It appears that the other non-zero phase value is $\frac 1 3$, so it will not give a solution either. I suppose that in this case you would need to choose a different value for $x$ and try again.

I think using a perfect square as $N$ violates some assumption of the proof that gcd($x^\frac r 2 -1, N$) or gcd($x^\frac r 2 +1, N$) divides $N$. This, I am sure, is why you cannot get the algorithm to work for $N=25$.
Edit: It appears to me that with $N$ a perfect square, every value of $x$ results in either a) an odd value of $r$, or b) $x^{\frac r 2} = -1 \text{ mod } N$. I do not have a proof for this, but I have not found a counter example either.
Edit: OK, here is the proof. The goal of the algorithm is to find an integer $y$ such that $y^2 = 1 \text { mod } N$ and $y \ne \pm1 \text { mod } N$. Suppose $N=p^2$ for some prime $p > 2$. Then $y^2-1 = (y+1)(y-1) = 0 \text { mod } N$, or equivalently, $p^2$ divides (y+1)(y-1). Then either $p$ divides both of the factors $y+1$ and $y-1$ or $p^2$ divides one of them. The first case implies that $p\le2$, contradiction. The second case implies $y = \pm 1 \text { mod } N$, contradiction.
This does not prevent the method from working on squares of composite numbers.

Possibly, this will also prevent you from finding a value of $x$ that works for $N=18=2(3^2)$. It seems to me that no value of $x$ works for that case.
Edit: The same kind of argument used for $N=p^2$ above also works for $N=kp^2$ where $k$ is an integer not divisible by $p$.

 

[Haorong Wu]

The continued fraction expansion is a way of finding a rational number close to a phase estimate produced in the order-finding algorithm. Since that algorithm operates on $t$ qubits, it only produces an approximation of the phase $\tilde \phi$. If you work through the continued fraction algorithm with $\tilde {s / r} = \frac {5461}{8192}$. You get successive rational numbers 0,1, $\frac 1 2$, $\frac 2 3$, $\frac {5461}{8192}$. So the closest rational number to $\tilde \phi$ other than $\frac {5461}{8192}$ itself is $\frac 2 3$, making $r=3$. In fact $7^3 = 1 \text{ mod } 18$, so it is the correct value for $r$. Unfortunately, it is not an even number, so it won't work for the rest of the algorithm. It appears that the other non-zero phase value is $\frac 1 3$, so it will not give a solution either. I suppose that in this case you would need to choose a different value for $x$ and try again.

I think using a perfect square as $N$ violates some assumption of the proof that gcd($x^\frac r 2 -1, N$) or gcd($x^\frac r 2 +1, N$) divides $N$. This, I am sure, is why you cannot get the algorithm to work for $N=25$.
Edit: It appears to me that with $N$ a perfect square, every value of $x$ results in either a) an odd value of $r$, or b) $x^{\frac r 2} = -1 \text{ mod } N$. I do not have a proof for this, but I have not found a counter example either.
Edit: OK, here is the proof. The goal of the algorithm is to find an integer $y$ such that $y^2 = 1 \text { mod } N$ and $y \ne \pm1 \text { mod } N$. Suppose $N=p^2$ for some prime $p > 2$. Then $y^2-1 = (y+1)(y-1) = 0 \text { mod } N$, or equivalently, $p^2$ divides (y+1)(y-1). Then either $p$ divides both of the factors $y+1$ and $y-1$ or $p^2$ divides one of them. The first case implies that $p\le2$, contradiction. The second case implies $y = \pm 1 \text { mod } N$, contradiction.
This does not prevent the method from working on squares of composite numbers.

Possibly, this will also prevent you from finding a value of $x$ that works for $N=18=2(3^2)$. It seems to me that no value of $x$ works for that case.
Edit: The same kind of argument used for $N=p^2$ above also works for $N=kp^2$ where $k$ is an integer not divisible by $p$.

Hi, tnich. Great ideas about the perfect squares. It would be an interesting topic on how to tackle those perfect squares, especially when $k$ is not $1$.

 

[tnich]

Hi, tnich. Great ideas about the perfect squares. It would be an interesting topic on how to tackle those perfect squares, especially when $k$ is not $1$.

$N=kn^2$ where $k$ is a special case. For any value of $r$ such that $x^r = 1 \text { mod } kn^2$, it is also true that $x^r = 1 \text { mod } n^2$. So about the best we can do with this method is obtain the factors k and $n^2$. However, we can also find the square root of each of those factors and determine whether it is an integer. It seems like that would resolve the issue.