Confusion Over Hydraulic Gradient, L parameter

[Typhon4ever]

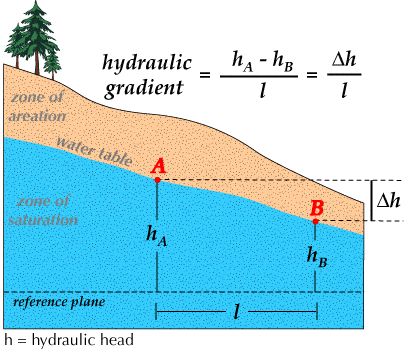
I've come across two different approaches to quantifying what l is in the equation for hydraulic gradient Δh/L. In this first picture L is the parallel distance along the datum across the reference plane

But in this second picture L is the length along the pipe

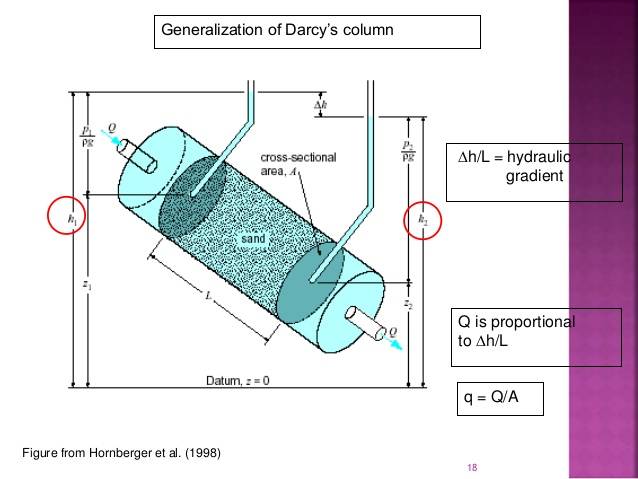
Why are the two L's different? I'm asking because there's a picture in a book of a sloping sand layer sandwiched between clay layers and L is taken to be like in the first image but the idea of a permeable sand layer between two effectively impermeable clay layers looks like the 2nd pipe image.

 

[Claudio Meier]

The correct interpretation is that of the second figure: the length to compute the gradient is that "travelled" by the water. After all, the hydraulic gradient is the spatial rate at which head (energy per unit weight of water) is lost or dissipated; basically: how many meters of head are lost per meter of distance travelled?

The first figure shows an unconfined aquifer in which the vertical scale is distorted or exaggerated; in most cases, the slope of unconfined aquifers is very flat, so that if one measures L in the horizontal, the difference with the actual distance traveled is negligible (because cosine of a small angle tends to 1, so that the horizontal distance will be almost equal to the length of the hypotenuse of the triangle).

Indeed, the Dupuit-Forchheimer assumption used to solve many groundwater and well problems assumes that flow is horizontal in unconfined aquifers, neglecting the small vertical component of the flow (by the way, note the irony: Dupuit means "of the well" in French).

Note that I wrote "travelled" between quotation marks above, because the actual distance takes the tortuosity of the flow paths into account, and we are not doing that here: our distances are measured assuming that there are no solid particles continuously deflecting the flow at the small scale.

Hope this helps,

Claudio Meier