rudransh verma
Gold Member
- 1,067
- 96
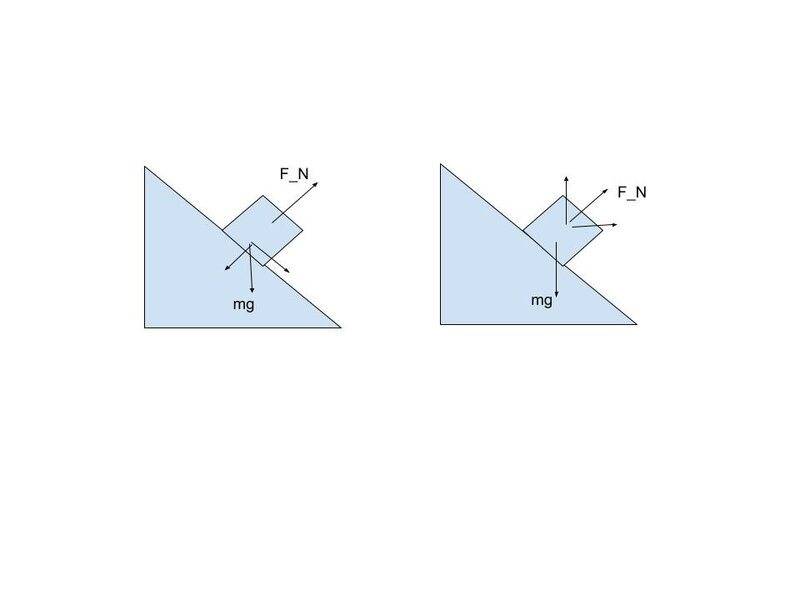
When we take the x-axis parallel to incline surface its clear that the horizontal component of weight is causing the block to come down but when we take the standard orientation its not so clear to me. Is horizontal component of ##F_N## causing the block to come down?
<Moderator's note: Use of external file sharing sites not allowed. Please upload all your images to PF.>
<Moderator's note: Use of external file sharing sites not allowed. Please upload all your images to PF.>
Last edited by a moderator:
