- #1
saltine
- 89
- 0
When you share charges between two identical capacitors (by letting half of the charges in one capacitor to spill to the other) the over energy is halved. Where does that energy go? In what way is it lost?
Example circuit:
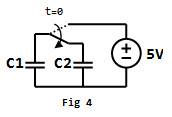
Before t=0, capacitor C1 is fully charged. The energy that it stores can be computed by E = 0.5QV. The voltage across the capacitor is 5volt. When the circuit toggles, half of its charges would spill to C2 (which is an identical capacitor). The voltage across either capacitor will be 2.5volt. The total energy after toggling is ETotal = 2( 0.5(0.5Q)(0.5V) ) = 0.5E. Half of the energy is lost.
But in what form is the energy "lost?"This is a similar situation using water tanks:
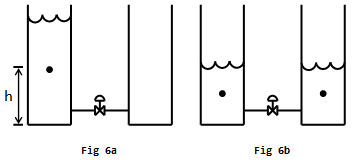
The potential energy in Fig6a is Ea = mgh. The potential energy in Fig6b is Eb = 2( (0.5m)g(0.5h) ) = 0.5 Ea. Half of the potential energy is lost.
When an object freefall, potential energy is converted into kinetic energy. So there is no net lost of energy. But where did the energy go in the case of the water tank? Is it true that the energy is still lost through kinetic energy, because, if the water must obviously move to get to the second tank, and while it is moving, there is additional kinetic energy (aside from its temperature), which the water gets from its potential energy?
What about the case of the capacitors? Is the energy lost simply because the charges moved (they moved because the potential energy gave them kinetic energy to move down the gradient)?
Does the energy lost have anything to do with electromagnetic radiation?
Example circuit:
Before t=0, capacitor C1 is fully charged. The energy that it stores can be computed by E = 0.5QV. The voltage across the capacitor is 5volt. When the circuit toggles, half of its charges would spill to C2 (which is an identical capacitor). The voltage across either capacitor will be 2.5volt. The total energy after toggling is ETotal = 2( 0.5(0.5Q)(0.5V) ) = 0.5E. Half of the energy is lost.
But in what form is the energy "lost?"This is a similar situation using water tanks:
The potential energy in Fig6a is Ea = mgh. The potential energy in Fig6b is Eb = 2( (0.5m)g(0.5h) ) = 0.5 Ea. Half of the potential energy is lost.
When an object freefall, potential energy is converted into kinetic energy. So there is no net lost of energy. But where did the energy go in the case of the water tank? Is it true that the energy is still lost through kinetic energy, because, if the water must obviously move to get to the second tank, and while it is moving, there is additional kinetic energy (aside from its temperature), which the water gets from its potential energy?
What about the case of the capacitors? Is the energy lost simply because the charges moved (they moved because the potential energy gave them kinetic energy to move down the gradient)?
Does the energy lost have anything to do with electromagnetic radiation?