Conservative Forces (gravity/voltage)

[Mr. Johnson]

In both voltage and gravity, I know that the work done in moving a particle between two points is independent of the path taken.

For my problem, it states "what if the path did make a difference?"

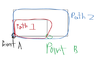
I'm suppose to design a device/machine that will move a particle or object repeatedly between two points, a to b and then back, where the energy necessary to go from a to b is half the energy that is returned when the mass moves from b to a long a different path. Also show that this device can do an unlimited quantity of useful work.

The question doesn't really state any parameters on the design.

We are learning about Kirchhoff's voltage law and how it was derived. I can't think of anything logical. Can anyone offer some advice?

Any help will be appreciated. Thank you.

 

[ideasrule]

I think the simplest design is just a wire that traces out the two paths from a to b. If you drill a hole into the mass, thread it onto the wire, and put it at b, it'll follow the wire indefinitely, going faster and faster every time it comes back to b. You can devise some mechanism to extract work from the kinetic energy of the mass.

 

[Mr. Johnson]

Im having trouble visualizing what you mean. Like this?

 

[gneill]

Suppose that gravity insulator existed and you happened to obtain a fairly large square sheet of it. It's property is such that the gravitational field above it (when it's lying flat on the ground) is cut in half. You place the sheet under one side of a ferris wheel. What happens?

 

[Mr. Johnson]

^^^ That would work except for the person on the ferris wheel is traveling through only one path in that scenario...

 

[gneill]

^^^ That would work except for the person on the ferris wheel is traveling through only one path in that scenario...

No, the path from bottom to top (a to b) is quite distinct from the path from top to bottom (b to a); they lie on different arcs of the circle described by the wheel.

 

[Mr. Johnson]

How/Why is it useful to have unequal energy in this scenario?

 

[gneill]

How/Why is it useful to have unequal energy in this scenario?

Why don't you analyze the motion of the wheel? Assume that it's symmetrical in terms of mass distribution.

 

[ideasrule]

How/Why is it useful to have unequal energy in this scenario?

Let's assume a massless Ferris wheel with a non-massless rider, to make things simpler. Also, the gravity insulator is oriented vertically, so that the left half is "above" the insulator and the right side is below it.

The person on the Ferris wheel would travel from the top to the bottom of the Ferris wheel along the right side, gaining kinetic energy E. He would then rise up to the top along the left side, losing kinetic energy E/2. He has just gained an energy of E/2 for free, out of nowhere. Further rotations of the wheel would give him E/2 each turn until the end of time.

 

[Mr. Johnson]

Thank you for thoroughly explaining. So this system would be useful because after every revolution, half of the previous kinetic energy is gained and the wheel gets faster and faster?