Conserved Momentum Problem: Finding Velocity of a Block on a Slope

[ippo90]

Homework Statement

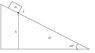
A box with mass m is on the top of a slope with angle alpha. Every surface has no friction. Assume that the system starts off from resting position. The start position of the box is P, and has a height h over the horizontal plane. Find the velocity of the block with the slope when the box has reached the horizontal plane ground. The mass of the slope block is M.

Homework Equations

-I believe that the relevant eq. are:
m₁v₁+m₂v₂=m₁v₁'+m₂v₂'

where v1' and v2' are the velocities after a collision etc.

-law of energy: 1/2mv²=mgh

-definitions of cosine and sine

-timeless eq for velocity: v²=v_o²+2as

The Attempt at a Solution

Because we are assuming that the system starts off from resting state, v₁ and v₂=0
hence mv₁'=(m+M)v₂' [they will move in different directions]

we want to find v₂'. Therefore I tried to express v₁' in terms of angle, height. It turned out to be all wrong. What did i do wrong?

I hope someone will help me with this. I've used like 3 hours or so..

thank you

 

[Doc Al]

-I believe that the relevant eq. are:
m₁v₁+m₂v₂=m₁v₁'+m₂v₂'

where v1' and v2' are the velocities after a collision etc.

OK.

-law of energy: 1/2mv²=mgh

OK, but be sure to consider the total energy of the system.

-definitions of cosine and sine

-timeless eq for velocity: v²=v_o²+2as

Not needed.

Because we are assuming that the system starts off from resting state, v₁ and v₂=0
hence mv₁'=(m+M)v₂' [they will move in different directions]

How did you arrive at this result from your conservation of momentum equation above?

 

[ippo90]

The equation used is this:
m₁v₁+m₂v₂=m₁v₁'+m₂v₂'

since the system starts from resting state v₁ (start velocity of box) and v₂(start velocity of the slope) are 0. this gives the equation:

m₁v₁'+m₂v₂'=0

the velocity of the box, when it reaches the end is v₁'. the momentum for the box will be m₁v₁'. for the slope the velocity will be -v₂' since it will probably move the opposite direction. the momentum will therefore be -(m+M)v₂' (since the box is still on the slope when reaching the ground).

hence I got that eq. Have I done a something wrong here?

 

[Doc Al]

The equation used is this:
m₁v₁+m₂v₂=m₁v₁'+m₂v₂'

since the system starts from resting state v₁ (start velocity of box) and v₂(start velocity of the slope) are 0. this gives the equation:

m₁v₁'+m₂v₂'=0

Good.

the velocity of the box, when it reaches the end is v₁'. the momentum for the box will be m₁v₁'.

Still good.

for the slope the velocity will be -v₂' since it will probably move the opposite direction.

You've already defined the velocity of the wedge to be v₂'. I suspect that you mean that v₂' will be in the opposite direction of v₁'. True!

the momentum will therefore be -(m+M)v₂' (since the box is still on the slope when reaching the ground).

No. This actually contradicts your equation above.

Hint: Just worry about the final speeds of everything after they part company.

 

[Doc Al]

Hint: Just worry about the final speeds of everything after they part company.

At least I assume that that's what they want. If I'm wrong, let me know. (They do give the angle alpha, which is not needed in my interpretation of the problem.)

 

[ippo90]

you mean like mv₁'=Mv₂'?

v₂'=mv₁'/M

BTW the answer does contain some cosine(alpha) and sine

 

[Doc Al]

you mean like mv₁'=Mv₂'?

v₂'=mv₁'/M

Yes.

BTW the answer does contain some cosine(alpha) and sine

That means that my assumption was wrong. They want the speed of the wedge when the sliding mass is still on the wedge, just when it reaches the bottom.

Sorry about that!

This is a bit more complicated.

Hint: Only the horizontal component of momentum is conserved.

 

[ippo90]

which means I have to find the x component of the box' velocity?

if so I used the energy law to calculate v when sliding down.

​

v=sqroot(2gh)

I used this to find v_x=vcos(a)=sqroot(2gh)cos(a)

am I on the right track?

 

[Doc Al]

which means I have to find the x component of the box' velocity?

It means you'll be using the x component of the box's velocity in your conservation of momentum equation.

if so I used the energy law to calculate v when sliding down.

​

v=sqroot(2gh)

I used this to find v_x=vcos(a)=sqroot(2gh)cos(a)

am I on the right track?

Careful. The potential energy of the box (mgh) is used to provide the total KE of box and slope.

 

[ippo90]

I don't think I got that.

What velocity do I find when I use this method? velocity of box relative to the slope?

if so how do I find the velocity I need?

I'm so stuck =P

 

[Doc Al]

I don't think I got that.

What velocity do I find when I use this method? velocity of box relative to the slope?

if so how do I find the velocity I need?

I'm so stuck =P

One way is to express the speed of the box relative to the slope as V. Then you write your conservation equations in terms of that. In the final analysis, all you care about is the speed of the slope.

In your conservation of energy equation, set the initial PE equal to the total KE of both box and slope.

I just cranked it out and I get quite a messy expression. (It wouldn't surprise me if I made an algebra error along the way. I'm multi-tasking. )

 

[ippo90]

the answer is supposed to be

v₂'²=2m²ghcos²(a)/[(M+m)(M+msin²(a))]

did you get this?

my attempt:
mgh=1/2mv²+1/2(M+m)v₂'²

where v is the velocity for the box when it gotten down (not in the x direction)

velocity in the x direction is:
v=v₁'/cos(a)

I plugged it into the eq. above and got a ugly eq. but it doesn't seem to be the same as the correct answer.

 

[Doc Al]

the answer is supposed to be

v₂'²=2m²ghcos²(a)/[(M+m)(M+msin²(a))]

did you get this?

Yes, exactly.

my attempt:
mgh=1/2mv²+1/2(M+m)v₂'²

where v is the velocity for the box when it gotten down (not in the x direction)

Is v the velocity of the box with respect to the slope or with respect to the ground?

You should have one term for m and another for M. You shouldn't have a term for (m+M).

velocity in the x direction is:
v=v₁'/cos(a)

If v is with respect to the slope you must also add in the speed of the slope when calculating the horizontal speed of the box with respect to the ground.

My recommendation:
Use V to represent the speed of the box with respect to the slope.
Let the speed of the slope be v₂' moving to the left.

Write the x-component of the speed of the box with respect to the ground.
Write the y-component of the speed of the box with respect to the ground.

Use the above speeds to write your conservation equations, for energy and horizontal momentum.

 

[ippo90]

to be honest, I'm totally lost now. why shouldn't I use (M+m)? the box is still on the slope.
I don't know how to use the velocity relative to the slope ='(

 

[Doc Al]

why shouldn't I use (M+m)?

That would work if the box and slope were moving together as one. But they are not. You have two masses, m and M, and they each have their own speed.

the box is still on the slope.

True, but the box moves with respect to the slope.

I don't know how to use the velocity relative to the slope

If you were riding along with the slope, you'd see the box move down the slope with some speed V. That's what it means.

What we need are the speeds with respect to the ground, so combine the speed of the slope with the speed of the box with respect to the slope to get an expression for the speed of the box with respect to the ground.

 

[ippo90]

ok I now understand that v(box)=v(rel)+v(slope).

if I now write the law for conservation of momentum, it will be:

(m+M)v_(slope)=m(v_(rel)+v_(slope))/cos(a)

 

[Doc Al]

ok I now understand that v(box)=v(rel)+v(slope).

OK. Realizing that v(slope) is horizontal, find the x component of v(box). What's the x component of v(rel)?

if I now write the law for conservation of momentum, it will be:

(m+M)v_(slope)=m(v_(rel)+v_(slope))/cos(a)

Again you combine m and M for some reason. All you need is this:
mv(box)_x + Mv(slope) = 0

Suggestion: If you call the speed (magnitude) of the slope v₂, then v(slope) = -v₂ (since the slope moves to the left). Let V = v(rel). Then you can express all needed speeds in terms of v₂ and V.

 

[ippo90]

even for the momentum you don't have to include both masses?

is it correct that v(box) and v(rel) have the same direction?
hence
v(box)x=v(box)cos(a)
and
v(rel)x=v(rel)cos(a)
??

 

[ippo90]

ok.. I've totally lost it.

what do I need to know to begin with?

 

[Doc Al]

even for the momentum you don't have to include both masses?

Why would you? You have two separate masses, each with its own speed.

is it correct that v(box) and v(rel) have the same direction?

No. v(rel) is parallel to the slope direction. So you can use trig functions and the angle to find its components.

Here you go:
v(box)x = v(rel)cos(a) + v(slope) = Vcos(a) - v₂
v(box)y = -v(rel)sin(a) = -Vsin(a)

So rewrite your conservation equations in terms of these.

 

[ippo90]

I somehow can't visualize the directions of v(box) and v(rel).

I tried to use the eq. from you post and got

Mv₂=mv_bx

and

mgh=1/2mv_bx²+1/2Mv₂²

this should be correct

 

[Doc Al]

I tried to use the eq. from you post and got

Mv₂=mv_bx

OK. But express it in terms of V and v₂.

and

mgh=1/2mv_bx²+1/2Mv₂²

Don't forget that the box has a y-component of velocity. And express it in terms of V and v₂.

 

[ippo90]

I really want to understand this, but it's really hard to visualize. This is a stupid request but is it OK if you upload a pic where you draw in the vector for v(rel) and v for the box? MS paint is good for me =)

 

[Doc Al]

I really want to understand this, but it's really hard to visualize. This is a stupid request but is it OK if you upload a pic where you draw in the vector for v(rel) and v for the box? MS paint is good for me =)

How about I try to describe it in words? We can worry about a diagram later.

At the time in question, when the box is at the bottom of the slope, let's describe the velocities:

A: The velocity of the slope with respect to the ground is horizontal and to the left. Let's call that v₂, going to the left. (Imagine an arrow pointing left, with magnitude v₂.)

B: The velocity of the box with respect to the slope is parallel to the slope. Call this vector v(rel) or V: imagine an arrow pointing down and to the right at an angle alpha below horizontal. This is just what you'd see if you were a bug riding along on the slope, watching the box slide; it's sliding down the slope, so of course its velocity is parallel to the surface of the slope. You can easily find the x and y components of this velocity since you know its direction.

C: The velocity of the box with respect to the ground, which we call v(box). To find this, we just add the first two velocities. Since we're adding a horizontal vector to the one slanting down at angle alpha, we end up with a vector that slants down and to the right at an angle greater than alpha with the horizontal. We can easily find the x and y components of this velocity by adding the components of the other velocities: Cx = Ax + Bx, etc.

This is similar to dropping a ball in a moving car. With respect to the car, the ball moves straight down. But with respect to the ground, the ball has an additional velocity due to the motion of the car itself.

I wouldn't get too concerned with visualizing all the details. What matters is that we can deal with things analytically.

The key is to realize that all our equations for energy and momentum conservation must use the speeds with respect to the ground. And we know how to find those and their components.

Let me know if this makes sense.

 

[ippo90]

That was a wonderful explanation, now everything makes sense!

earlier I thought that v(box) was pointing the same direction as the slope, and v(rel) was pointing with ''the angle + a little more''.

now I will try and see if I arrive at the correct answer=)

 

[ippo90]

Now I know that MV=mv(bx) where v(bx) is the velocity of the box from the ground.

v(b) can be expressed like this:
v(bx)=v(rel)cos(a)+V
and
v(by)=-v(rel)sin(a)

we also know that:
mgh=1/2mv(bx)²+1/2mv(by)²+1/2MV²

but the algebra is so hard.

But the analysis is correct?

 

[Doc Al]

Now I know that MV=mv(bx) where v(bx) is the velocity of the box from the ground.

Good.

v(b) can be expressed like this:
v(bx)=v(rel)cos(a)+V

Looks like you're using V to represent the speed of the slope. (What we used to call v₂; no problem.) Since it moves to the left, I would write this as:
v(bx)=v(rel)cos(a) - V

and
v(by)=-v(rel)sin(a)

Good.

we also know that:
mgh=1/2mv(bx)²+1/2mv(by)²+1/2MV²

Good.

but the algebra is so hard.

But the analysis is correct?

So far, so good. The next step is to replace all instances of v(bx) and v(by) with their equivalents in terms of V and v(rel). Then your momentum and energy equations will be ready to go.

Then you just need the stamina to grind it out. Sure it's a pain in the butt. But whatever doesn't kill you makes you stronger!

Hints: First expand the energy equation. Then use the momentum equation to solve for v(rel) and substitute what you find in the expanded energy equation. Don't give up now.

[Sorry for the delayed response. I've been tied up with real work. ]

 

[ippo90]

Yay! I did it, thanks to you! =)

Thank you for having such patience with me. You're awesome ^^

 

[Doc Al]

That's what I like to hear. Good work!