Kqwert
- 160
- 3
Homework Statement
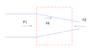
I have a situation as illustrated by the image above, where the red box illustrates the CV. The pressure on the left side of CV is P1, while the pressure on the right side of CV is P2. Here I´ve directed the pressure forces acting inwards on CV. The problem arises with Fk. I am interested in the force acting from the water ON the wall. Sum of forces in x-direction:
Fsigma = P1*A1 + Fk - P2*A2.
The answer manual however want´s Fk to be negative. Where am I wrong?
Attachments
Last edited: