- #1
Happiness
- 679
- 30
Consider a sequence with the ##n^{th}## term ##u_n##. Let ##S_{2m}## be the sum of the ##2m## terms starting from ##u_N## for some ##N\geq1##.
If ##\lim_{N\rightarrow\infty}S_{2m}=0## for all ##m##, then the series converges. Why?
This is not explained in the following proof:

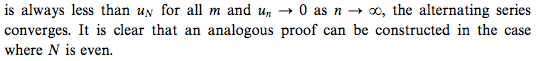
If ##\lim_{N\rightarrow\infty}S_{2m}=0## for all ##m##, then the series converges. Why?
This is not explained in the following proof:
Last edited: