Coordinate systems parameterized by pseudo arc-length

[member 428835]

Hi PF!

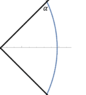
Can anyone help me define a coordinate system for a circular arc that makes a specified angle $\alpha$ with a 90 degree wedge? See picture titled Geo.

As an example, a circular arc can be parameterized over a straight line by $s$, making angle $\alpha$, via $$\vec T = \left\langle \frac{\sin(s)}{\sin\alpha}, \frac{\cos (s) - \cos \alpha }{\sin\alpha} \right\rangle$$

 

[BvU]

Hi,

define a coordinate system

are you defining a cordinate system, or are you searching for a parametrization ?

I like to keep things simple and pick an easy example, e.g. $\alpha = {\pi\over 2}$, Now $$\vec T = (\sin s, \cos s) $$ is a quarter circle with radius 1 and centered at the origin. For $s\in [0, {\pi\over 2}]$ oriented clockwise.

But it's a parametrization in a cartesian coordinate system.

 

[member 428835]

Hi,
are you defining a cordinate system, or are you searching for a parametrization ?

Sorry, a parametrization!

I like to keep things simple and pick an easy example, e.g. $\alpha = {\pi\over 2}$, Now $$\vec T = (\sin s, \cos s) $$ is a quarter circle with radius 1 and centered at the origin. For $s\in [0, {\pi\over 2}]$ oriented clockwise.

But it's a parametrization in a cartesian coordinate system.

Yep, this is simple, but what if I want $\alpha \neq 90^\circ$?

 

[BvU]

Simplest case: center of circle moves along $y=x$. (If you want to restrict to a single $\alpha$)
And you have to do some trig to find the domain of $s$.