Coordinate translation on a rotating plane

[newjerseyrunner]

I have this problem where I need to convert from mouse coordinates on the screen with relative coordinates on an object that can be arbitrarily translated, scaled, and rotated around another arbitrary position. I've already normalized all of the units to be the same (pixels) but the trig is eluding me right now.

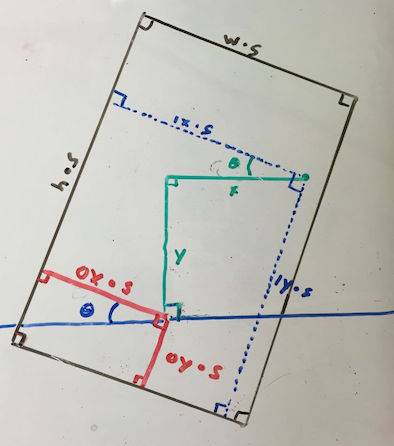
h - height of normalized object
w - width of normalized object
s - scalar
theta - rotation angle
(ox, oy) - the point at which the object rotates
(x, y) - the point along absolute horizontal and vertical from the rotation point
(ix, iy) - the unknown

the blue line is the absolute horizontal, but it's value is arbitrary
theta, x, y, ix, iy, ox, and oy are real numbers
w, h, s are positive real numbers

ix = (ox * s + acos(90 - theta) * y + acos(theta) * x) / s;
iy = (oy * s + asin(90 - theta) * y + asin(theta) * x) / s;
Is that right?

 

[andrewkirk]

There are three operations being performed: rotation, scaling and translation. The result depends on the order of operations, and so the formula will also depend on that.

What is the order of the three operations?