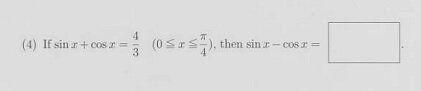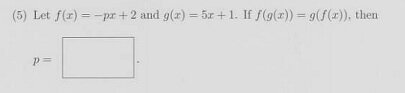MHB Correcting Resolutions: Is it Right?

[squexy]

´
Could anyone tell me if the resolutions of these questions are correct?View attachment 3754

Cosx = 4/3 - sin x

Six - 4/3 - Sin x = 0
2 Sinx = 4/3
Sinx = 4/6

Cosx = 4/3 - 4/6
Cosx = 8/6 - 4/6
Cosx = 4/6
View attachment 3755

G(x) = 5x + 1
5*(px+2)+1
5px + p = 5px + 10+ 1
p = 11

 

[MarkFL]

For the first one, I would begin with the given:

$$\sin(x)+\cos(x)=\frac{4}{3}$$

Square it:

$$\sin^2(x)+2\sin(x)\cos(x)+\cos^2(x)=\frac{16}{9}$$

Apply a Pythagorean identity:

$$2\sin(x)\cos(x)+1=\frac{16}{9}$$

$$2\sin(x)\cos(x)=\frac{7}{9}$$

Now, let:

$$\sin(x)-\cos(x)=a$$

Square this, apply a Pythagorean identity, use the result above, and take the appropriate root for $a$...what do you find?

 

[MarkFL]

For the second problem, we find:

$$f(g(x))=-p(5x+1)+2$$

$$g(f(x))=5(-px+2)+1$$

Hence:

$$-p(5x+1)+2=5(-px+2)+1$$

Solving for $p$, what do you find?

 

[squexy]

For the first one, I would begin with the given:

$$\sin(x)+\cos(x)=\frac{4}{3}$$

Square it:

$$\sin^2(x)+2\sin(x)\cos(x)+\cos^2(x)=\frac{16}{9}$$

Apply a Pythagorean identity:

$$2\sin(x)\cos(x)+1=\frac{16}{9}$$

$$2\sin(x)\cos(x)=\frac{7}{9}$$

Now, let:

$$\sin(x)-\cos(x)=a$$

Square this, apply a Pythagorean identity, use the result above, and take the appropriate root for $a$...what do you find?

Sin^2 x -2(sinx . cosx) + cos^2(x)= a^2

-2(sinx . cosx) + 1= a^2
- 2(six . cosx) = a^2 - 1
7/9 = - a^2 + 1
7/ 9 -9/9 = a^2
2/9 = -a^2
a = √-2/9

For the second problem, we find:

$$f(g(x))=-p(5x+1)+2$$

$$g(f(x))=5(-px+2)+1$$

Hence:

$$-p(5x+1)+2=5(-px+2)+1$$

Solving for $p$, what do you find?

-5px - p = -5px +10 + 1
- p = 11
p = - 11

 

[MarkFL]

For the first one, you get to:

$$a^2=\frac{2}{9}$$

Observing that on $$0\le x\le\frac{\pi}{4}$$ we have:

$$\cos(x)\ge\sin(x)\implies 0\ge\sin(x)-\cos(x)$$ we then know we have to take the negative root:

$$a=-\frac{\sqrt{2}}{3}$$

For the second one, check your algebra...your result is incorrect as you forgot about the 2 on the left side.

 

[squexy]

For the first one, you get to:

$$a^2=\frac{2}{9}$$

Observing that on $$0\le x\le\frac{\pi}{4}$$ we have:

$$\cos(x)\ge\sin(x)\implies 0\ge\sin(x)-\cos(x)$$ we then know we have to take the negative root:

$$a=-\frac{\sqrt{2}}{3}$$

For the second one, check your algebra...your result is incorrect as you forgot about the 2 on the left side.

-5px - p +2 = -5px +10 + 1
- p = 9
p = - 9

 

[MarkFL]

-5px - p +2 = -5px +10 + 1
- p = 9
p = - 9

Yes, that's correct. (Yes)

 

[Prove It]

´
Could anyone tell me if the resolutions of these questions are correct?View attachment 3754

Cosx = 4/3 - sin x

Six - 4/3 - Sin x = 0
2 Sinx = 4/3
Sinx = 4/6

Cosx = 4/3 - 4/6
Cosx = 8/6 - 4/6
Cosx = 4/6
View attachment 3755

G(x) = 5x + 1
5*(px+2)+1
5px + p = 5px + 10+ 1
p = 11

As an alternative to Question 1, it is possible to write a linear combination $\displaystyle \begin{align*} a\sin{(x)} + b\cos{(x)} = c\sin{ \left( x + \varphi \right) } \end{align*}$, where $\displaystyle \begin{align*} c = \sqrt{a^2 + b^2} \end{align*}$. Don't believe me? Well in your case, $\displaystyle \begin{align*} a = b = 1 \end{align*}$, so $\displaystyle \begin{align*} c = \sqrt{1^2 + 1^2} = \sqrt{2} \end{align*}$. Thus

$\displaystyle \begin{align*} \sqrt{2}\sin{ \left( x + \varphi \right) } &= \sin{(x)} + \cos{(x)} \\ \sqrt{2} \left[ \sin{(x)}\cos{(\varphi )} + \cos{(x)} \sin{ \left( \varphi \right) } \right] &= \sin{(x)} + \cos{(x)} \\ \sqrt{2}\sin{(x)}\cos{(\varphi )} + \sqrt{2}\cos{(x)}\sin{(\varphi )} &= \sin{(x)} + \cos{(x)} \end{align*}$

So that means $\displaystyle \begin{align*} \sqrt{2}\cos{ (\varphi )} = 1 \end{align*}$ and $\displaystyle \begin{align*} \sqrt{2}\sin{( \varphi )} = 1 \end{align*}$. It should be pretty obvious then that $\displaystyle \begin{align*} \varphi = \frac{\pi}{4} \end{align*}$.

Thus $\displaystyle \begin{align*} \sin{(x)} + \cos{(x)} = \sqrt{2} \sin{ \left( x + \frac{\pi}{4} \right) } \end{align*}$. So now we should be able to solve the problem...

$\displaystyle \begin{align*} \sin{(x)} + \cos{(x)} &= \frac{4}{3} \\ \sqrt{2} \sin{ \left( x + \frac{\pi}{4} \right) } &= \frac{4}{3} \\ \sin{ \left( x + \frac{\pi}{4} \right) } &= \frac{4}{3\,\sqrt{2}} \\ \sin{ \left( x + \frac{\pi}{4} \right) } &= \frac{ 4\,\sqrt{2}}{3 \cdot 2 } \\ \sin{ \left( x + \frac{\pi}{4} \right) } &= \frac{2\,\sqrt{2}}{3} \\ x + \frac{\pi}{4} &= \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \\ x &= \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } - \frac{\pi}{4} \end{align*}$

Now you should be able to find $\displaystyle \begin{align*} \sin{(x)} - \cos{(x)} \end{align*}$, but it will look absolutely horrible...

$\displaystyle \begin{align*} \sin{(x)} - \cos{(x)} &= \sin{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } - \frac{\pi}{4} \right] } - \cos{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } - \frac{\pi}{4} \right] } \\ &= \sin{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \cos{ \left( \frac{\pi}{4} \right) } - \cos{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \sin{ \left( \frac{\pi}{4} \right) } - \left\{ \cos{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \cos{ \left( \frac{\pi}{4} \right) } + \sin{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \sin{ \left( \frac{\pi}{4} \right) } \right\} \\ &= \frac{2\,\sqrt{2}}{3} \cdot \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}}\cos{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } - \left\{ \frac{1}{\sqrt{2}} \cos{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } + \frac{2\,\sqrt{2}}{3} \cdot \frac{1}{\sqrt{2}} \right\} \\ &= \frac{2}{3} - \frac{1}{\sqrt{2}} \,\sqrt{ 1 - \left\{ \sin{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \right\} ^2 } - \left( \frac{1}{\sqrt{2}} \,\sqrt{ 1 - \left\{ \sin{ \left[ \arcsin{ \left( \frac{2\,\sqrt{2}}{3} \right) } \right] } \right\} ^2 } + \frac{2}{3} \right) \\ &= \frac{2}{3} - \frac{1}{\sqrt{2}}\,\sqrt{ 1 - \left( \frac{2\,\sqrt{2}}{3} \right) ^2 } - \left[ \frac{1}{\sqrt{2}} \,\sqrt{ 1 - \left( \frac{2\,\sqrt{2}}{3} \right) ^2 } + \frac{2}{3} \right] \\ &= \frac{2}{3} - \frac{1}{\sqrt{2}}\,\sqrt{ 1 - \frac{8}{9} } - \left[ \frac{1}{\sqrt{2}}\,\sqrt{ 1 - \frac{8}{9} } + \frac{2}{3} \right] \\ &= \frac{2}{3} - \frac{1}{\sqrt{2}} \,\sqrt{\frac{1}{9}} - \left[ \frac{1}{\sqrt{2}}\,\sqrt{\frac{1}{9}} + \frac{2}{3} \right] \\ &= \frac{2}{3} - \frac{1}{\sqrt{2}}\cdot \frac{1}{3} - \frac{1}{\sqrt{2}}\cdot \frac{1}{3} - \frac{2}{3} \\ &= -\frac{2}{3\,\sqrt{2}} \\ &= -\frac{\sqrt{2}}{3} \end{align*}$

 

[Dethrone]

Amazing! (Cool)
Your mistake was so subtle that even though I tracked the precise location of your mistake with my calculator, I could not pinpoint where it occurred!

$$\displaystyle \begin{align*} &= \frac{2}{3} - \frac{1}{\sqrt{2}} \,\sqrt{\frac{1}{9}} - \left[ \frac{1}{\sqrt{2}}\,\sqrt{\frac{1}{9}} + \frac{2}{3} \right] \\ &= \color{red}\frac{2}{3} - \frac{1}{\sqrt{2}}\,\frac{1}{\sqrt{3}} - \frac{1}{\sqrt{2}}\,\frac{1}{\sqrt{3}} - \frac{2}{3} \\ &= -\frac{2}{\sqrt{6}} \\ &= -\frac{2\,\sqrt{6}}{6} \\ &= -\frac{\sqrt{6}}{3} \end{align*}$$

$$\sqrt{\frac{1}{9}}=\frac{1}{3}\ne \frac{1}{\sqrt{3}}$$
:D

 

[Prove It]

Amazing! (Cool)
Your mistake was so subtle that even though I tracked the precise location of your mistake with my calculator, I could not pinpoint where it occurred!$$\sqrt{\frac{1}{9}}=\frac{1}{3}\ne \frac{1}{\sqrt{3}}$$
:D

Typical, I can do mathemagic and can't do basic arithmetic >_< hahaha will edit now (y)

 

[chisigma]

A more general solution to the problem which also does not require trigonometry equation...

$\displaystyle \sin x + \cos x = \frac{4}{3}\ (1)$

... consists in placing $\sin x = y$ and this leads to the equation...

$\displaystyle y + \sqrt{1 - y^{2}} = \frac{4}{3}\ (2)$

The solution of (1) is immediate ...

$\displaystyle y = \sin x = \frac{2}{3} \pm \frac{\sqrt{2}}{6}\ (3)$

Looking at the (1) it turns out that $\sin x$ and $\cos x$ that they can be exchanged between them and that means also that is...

$\displaystyle \sin x - \cos x = \pm \frac{\sqrt{2}}{3}\ (4)$

Kind regards

$\chi$ $\sigma$