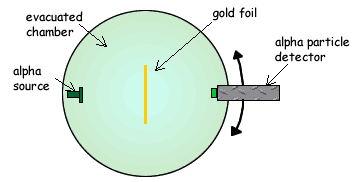
The differential scattering cross section for the whole target (assuming the alpha particle beam illuminated the whole target) is given by ## \\ ## ## \frac{d \sigma}{d \Omega}=\frac{(\frac{d N_{sc}}{dt \, d \Omega})}{(\frac{d N_{inc}}{dt \, d \sigma})} ## . (Note that ## N_{sc}=N_{inc} ##, i.e. there is a one-to-one mapping between incident particles and scattered particles. Any particles that go in the forward direction, essentially unscattered, are included in the mathematics. Notice also how ## d \sigma ## goes from the denominator of the denominator(on the right side of the equation) to the numerator (on the left side of the equation), and ## d \Omega ## in the denominator of the numerator winds up in the denominator.) ## \\ ## Now ## d \Omega=\frac{A_{receiver}}{R^2} ## where ## R ## is the distance to the receiver from the target. (Here we are computing the solid angle that the receiver subtends.) This should allow you to compute ## \frac{dN_{sc}}{dt \, d \Omega} ##. It is ok that you only measured in one plane at an angle ## \theta ## off-axis. One thing you need to determine is where Rutherford's ## \theta ## is measured from, i.e. if it gets scattered back at you, is ## \theta =0 ## or is ## \theta=180 ## for this case? ## \\ ## In addition, ## \frac{d N_{inc}}{(dt \, d\sigma)}=\frac{d N_{inc}}{(dt \, A_{receiver})} ##. (I assume you initially put the receiver at the target and measured the counts per second, etc.) ## \\ ## Putting it all together, you should be able to compute ## \frac{d \sigma}{d \Omega} ## as a function of ## \theta ##. This will give you ## \frac{d \sigma}{d \Omega} ## for the whole target. If you want to compute ## \frac{d \sigma}{d \Omega} ## for a single gold atom, you need to know how many atoms are in your target and divide by this number. ## Number \, of \, atoms=[\frac{(mass \, in \, grams \, of \, target)}{(A.W._{gold})}]6.02 E+23 ##. ## \\ ## Editing: One additional note: If you want to get an estimate of the size (area) of the scatterer ## \sigma ##, i.e. of a single atom, you can take integrate ## \frac{d \sigma}{d \Omega} ## for a single atom over the ## 4 \pi ## solid angle, leaving off the unscattered part. i.e. ## \sigma=\int \frac{d \sigma}{d \Omega} \, sin(\theta) \, d \theta \, d \phi ##. (For the case of scattering off of a solid target, e.g. bee-bees incident on a hard spherical target, this last formula is quite precise, but for the case of an inverse square law type force that gets screened by electrons, etc., computing ## \sigma ## is simply an approximation. Notice for the case of bee-bees onto a hard spherical target, why you would not count anything that was unscattered=i.e. that missed the target. The computation for ## \sigma ## for this case gives the projected area of the target, i.e. ## \sigma= \pi a^2 ## where ## a ## is the radius of the spherical target.) ## \\ ## I could mention one additional item that might be of interest about the mathematics of the scattering theory. Essentially, there is a mapping of regions in the incident plane ## \sigma ## to regions ## \Omega ## i.e. locations ## \Omega (\theta, \phi) ## of the space of the scattered beam. Thereby the function ## \frac{d \sigma }{d \Omega} ## can be computed if one knows how the particles, such as bee-bees, get scattered off of the hard spherical target. i.e. where they wind up in the scattered space depends precisely on where they hit the target. ## \sigma ## maps into ## \Omega ##. The ## \sigma(r) ## can be viewed as any ## \sigma ## inside a radius of ##r ##, and the ## \Omega(\theta,\phi) ## as anything inside the cone. Then ## \frac{d \sigma}{d \Omega} ## is how fast the ## \sigma ## region changes compared to the scattered cone ## \Omega ##.