Could someone me to read the following line

[EnglsihLearner]

Could someone please help me to read the following line(in case of inner product)?

 

[jbunniii]

The statement indicates that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$. This means that to each ordered pair $(u,v)$ with $u,v \in V$, it assigns an element $\langle u,v \rangle$ in $F$.

Presumably $F$ is a field, and $V$ is a vector space over $F$.

 

[EnglsihLearner]

The statement indicates that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$.

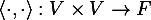
Yes, I understand now. Could you please explain what does "map" mean here?As I know map means the following-

https://www.google.com.bd/search?bi....0..0.0...0...1c.1.24.serp..3.0.0.hrQDtAr7Tpw

If it is same here then I would request you to explain again the following part-

that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$

 

[jbunniii]

Yes, I understand now. Could you please explain what does "map" mean here?

In mathematics, "map" and "function" mean the same thing.

 

[blue_raver22]

Sure, I would be happy to assist you in understanding the concept of inner product. An inner product is a mathematical operation that takes two vectors and produces a scalar value. It is often denoted as <x,y>, where x and y are vectors. The inner product is calculated by multiplying the corresponding elements of the two vectors and then summing them together. For example, if we have two vectors, x = [1, 2, 3] and y = [4, 5, 6], the inner product would be <x,y> = 1*4 + 2*5 + 3*6 = 32. The inner product is commonly used in linear algebra and has applications in various fields such as physics, engineering, and computer science. I hope this helps to clarify the concept for you. Let me know if you have any further questions.