Coulomb's Forces triangle of charges

[pumpernickel]

Homework Statement

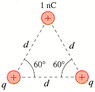
Consider the triangle of charges diagrammed below, for which d = 5 cm, q = 2 nC, and the +x-axis points to the right. What is the force Fvec on the 1 nC charge? Give your answer as a magnitude and a direction.

Homework Equations

F=K(q)(Q)/r^2

The Attempt at a Solution

I am not sure what to do. I converted the nc to c, and the cm to m. Then I did

F= K(1X10^-9)(2X10^-9)/.05^2

Then I would multiply this by two because the two sides are effecting the charge. Is this on the right track?

Thanks

 

[electricspit]

Remember that the force acting on the one particle is the sum of the individual forces acting on that one particle.

\vec{F}=\frac{q_i}{4\pi\epsilon_0}\sum\limits_{j=0, j\neq{i}}^n \frac{q_j \hat{r_{ji}}}{|r^2|}

Where q_i is the particle which is experiencing the force, n is the total number of particles, \hat{r_{ji}} is the unit vector pointing from j to i.

If this formula is confusing or you haven't seen it before, I can explain it more simply (i.e. if you are in high school, or first year physics).

 

[Simon Bridge]

That certainly looks like a secondary school or freshman college diagram.
You already know how to find the force on one charge due to another one.
You realized that you have to add the forces and noticed that the two forces you have to add are the same.

But you have forgotten that force is a vector - how do you add vectors?

 

[pumpernickel]

Well to add vectors you just add them keeping in mind direction, and in this case both sides of the triangle would have the same vector.

Wait, do you have to find the x and y components of the vector, and use those?

 

[Simon Bridge]

You can do that, or add them head-to-tail.

 

[BiGyElLoWhAt]

ok its an equilateral triangle, and you're looking at the forces on the top. what does that say about the forces in the x direction? I don't think head to tail is good enough for this problem, i think the prof wants a number. add F1 + F2 like this <F1x, F1y,F1z> + <F2x,F2y,F2z> = sum F on 1nC
z's are 0. so: <F1x, F1y,0> + <F2x,F2y,0>

 

[Simon Bridge]

I don't think head to tail is good enough for this problem, i think the prof wants a number.

What are you talking about? head-to-tail gets you a number just fine!
Sketch it out and see ;)

 

[patrickmoloney]

The net force component along the x-axis points rightward. With $\theta = 60°$

let $q_1 = 1nC$ , $q_2$ and $q _3 = 2nC$

$F_1 = 2\frac{q_1 q_2 cos\theta}{4\pi \epsilon a^2}$

Since $cos(60°) = \frac{1}{2}$ , we can write the expression as

$F_1 = \frac{k q_1 q_2}{a^2} = \frac{(8.99*10^{9} N\cdot m^2/C^2)(1.00*10^{-9} C)(2.00*10^{-9} C)}{(5*10^{-2} m)^2 } = 7.19*10^{-6} N$

 

[BiGyElLoWhAt]

The net force component along the x-axis points rightward.

you do realize we're calculating the force on the 1 nC, right? there is no x component to the force. it's zero. ∑F_{on1nC} = ∑K\frac{q_{j}q_{top}}{r^2}\hat{r}
= K[(\frac{q_{LowerLeft}q_{top}}{r^2}(cos(\theta)\hat{i} + sin(\theta) \hat{j})) + (\frac{q_{LowerRight}q_{top}}{r^2}(cos(\pi-\theta)\hat{i} + sin(\pi-\theta) \hat{j}))] (the angles are mirrored over \frac{\pi}{2})
= 0\hat{i} + 2K(\frac{q_{LowerLeft}q_{top}}{r^2}sin(\theta))\hat{j}

 

[BiGyElLoWhAt]

i guess i could've used d's instead of r's and plugged in the angles, but you get the picture.

 

[patrickmoloney]

I thought from symmetry, the net force component in the y-axis is zero. Not the x-axis, no?

 

[BiGyElLoWhAt]

step back from the maths and stuff and just think about it physically. From the picture, is the y force (vertical) component going to be zero on the top charge?

The bottom left charge exerts some force on the top up and to the right, and the bottom right charge exerts some force on the top up and to the left. since the distance, charge and angle are the same, the left and right components are equal yet opposite, and thus cancel.

 

[patrickmoloney]

Damn, they do cancel. I was thinking of different bottom charges.

 

[BiGyElLoWhAt]

damn, they do cancel. I was thinking of different bottom charges.

xd
=]