Cross product and dot product of forces expressed as complex numbers

[magwas]

Homework Statement

I have came up with an example to illustrate my question.

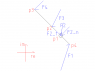
There is a rod, which can turn around p1.

p1p2 = (-1+j) m
p1p3 = (-3 + 3j) m
p1p4 = (1 - j ) m
F1 = (1+3j) N
F3 = (-1 - 2j ) N
F4 = unknown, orthogonal to the rod

compute F2_n, orthogonal component of F2 to the rod
compute F2_t, parallel component of F2 to the rod

Homework Equations

The question is actually here:
The sum of moments is
$$\sum{\vec{F} \times \vec{l}} =0$$
Where
$$a \times b = \Re{a} \Im{b} - \Im{a} \Re{b}$$
Is that true?
Likewise, the force components parallel to the rod is:
$$\sum{\vec{F} \cdot \hat{\vec{l}}} = 0$$
where
$$a \cdot b = a \overline{b} + b \overline{a} = 2 \Im{a} \Im{b} + 2 \Re{a} \Re{b}$$
Is it correct?

The Attempt at a Solution

I write the moments around p3. I sum here because:

• all forces are on the same side of the turning point
• all arms are measured towards the turning point (this is why p1p3 - p1p4)
• the direction of forces are encoded in their vectors

The unit vector normal to the rod is come by dividing a vector along the rod by its length, and multiplying it with j: $$\frac{\mathbf{\imath} p1p3}{\lvert{p1p3}\rvert}$$
so the equation for moments:
$$F_{1} \times \left(p1p3 - p1p4\right) + F_{3} \times \left(p1p3 - p1p2\right) + p1p3 \times \left \frac{\mathbf{\imath} p1p3}{\lvert{p1p3}\rvert} \lvert F_{2_{n}}\rvert} = \\<br /> <br /> \Im{p1p3} \Im\left(\frac{\lvert F_{2_{n}}\rvert p1p3}{\lvert{p1p3}\rvert}\right) + \Im\left(p1p3 - p1p2\right)<br /> \Re{F_{3}} + \Im\left(p1p3 - p1p4\right) \Re{F_{1}} + \Re{p1p3} \Re<br /> \left(\frac{\lvert F_{2_{n}}\rvert p1p3}{\lvert{p1p3}\rvert}\right) - \Im{F_{1}} \Re\left(p1p3 - p1p4\right) - <br /> \Im{F_{3}} \Re\left(p1p3 - p1p2\right) = \\<br /> <br /> 10.0 + 4.24264068711929 \lvert F_{2_{n}} \rvert = 0$$
so
$$\lvert F_{2_{n}}\rvert =-2.3570226039551$$ which gives
$$F_{2_{n}} = \lvert F_{2_{n}}\rvert \frac{\mathbf{\imath} p1p3}{\lvert{p1p3}\rvert} = 1.66666666666667 + 1.66666666666667 \mathbf{\imath}$$

Now the forces parallel to the rod:

We use our unit vector $$\hat{l} = \frac{p1p3}{\lvert{p1p3}\rvert}$$
, and forget F4 as it is orthogonal to the rod, so the sum:
$$F_{3} \cdot \hat{l} + \lvert F_{2_{t}}\rvert \cdot \hat{l} + F_{1} \cdot \hat{l} = \\<br /> 2 \lvert F_{2_{t}}\rvert \Re{\hat{l}} + 2 \Im{F_{1}} \Im{\hat{l}} + 2 \Im{F_{3}} \Im{\hat{l}} +<br /> 2 \Re{F_{1}} \Re{\hat{l}} + 2 \Re{F_{3}} \Re{\hat{l}} = \\<br /> 1.4142135623731 - 1.4142135623731 \lvert F_{2_{t}}\rvert = 0$$
so
$$\lvert F_{2_{t}}\rvert = 1$$
which gives
$$F_{2_{t}} = -0.707106781186548 + 0.707106781186548 \mathbf{\imath}$$
and
$$F_{2} = F_{2_{n}} + F{2_{t}} = 0.959559885480119 + 2.37377344785321 \mathbf{\imath}$$

 

[magwas]

Well, maybe I should have used $$magnitude_{F_{2_{n}}}$$ instead of $$\lvert F_{2_{n}}\rvert$$...

 

[nvn]

magwas: I got F2n = 2.3570 N, but I got F2t = 0.707 107 N, not 1. You can check your answer by summing forces in the rod tangential direction, to see if the summation equals zero.

 

[magwas]

I see, $$\lvert F_{2_{t}}\rvert \cdot \hat{l}$$ was a mistake.
the equation correctly is $$F2t + \left ( F_{1} \cdot l \right) + \left ( F_{3} \cdot l \right) = 0$$
but it comes down to
$$F2t + 2 \Im{F_{1}} \Im{l} + 2 \Im{F_{3}} \Im{l} + 2 \Re{F_{1}} \Re{l} + 2 \Re{F_{3}} \Re{l} = 0$$
which leads to $$1.4142135623731 + F2t = 0$$,
so F2t = -1.4142135623731
Do I have a problem with the definition of complex dot product?

Thank you again.

 

[magwas]

I have looked up the definition of vector dot product. Wikipedia tells me that it is
$$\sum a_{i} b_{i}$$ for vectors a=(a1,...,an) and b=(b1,...bn).

So a . b must be re(a)re(b)+im(a)im(b), not twice that.
In this way I get the same result as you, I believe.