Is there a connection between EPR and crossing symmetry in Feynman diagrams?

[stevendaryl]

This is sort of a nebulous question, but I'm wondering if anyone knows of analysis of the EPR experiment from the point of view of crossing symmetry for Feynman diagrams?

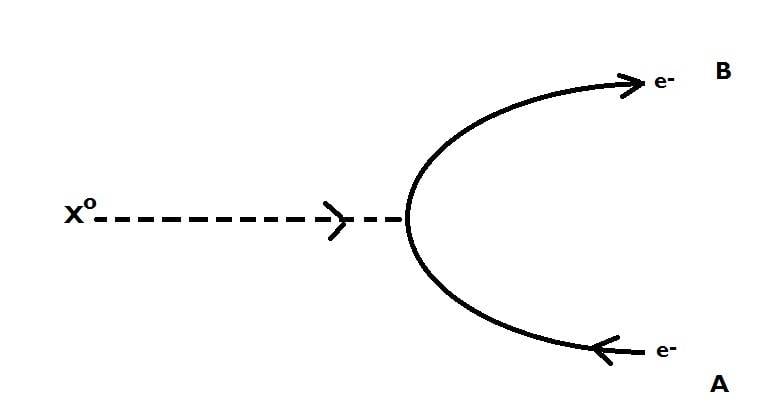
In the above diagram, I've drawn a very simple particle interaction diagram. The same diagram can be interpreted in two different ways, and the corresponding amplitudes are related in some analytic way that I'm not going to get into the details of. The two different ways are:

1. A neutral, massive, spin-zero particle, $X^0$ (not supposed to be any specific particle, but maybe you can think of it as a neutral pion) collides with an electron, and is absorbed, deflecting the electron.
2. The $X^0$ particle decays into an electron/positron pair.

These are, from the point of view of quantum field theory, very similar processes, which is why they have very similar Feynman diagrams. But now, I'd like to analyze these from the point of spin measurements at points $A$ and $B$ in the diagram.

In the first interpretation, we measure the spin of the electron at point $A$, along some axis, $\vec{A}$ and find in say spin-up in that direction. Later, at point $B$, we measure the spin along a second axis, $\vec{B}$. Assuming that the original $e^{-1}, X^0$ system had orbital angular momentum zero (I'm not sure how you might insure that this is true...which might be a weakness of my argument, such as it is), then we can use conservation of total angular momentum to conclude that the electron's spin doesn't change between points $A$ and $B$. So the probability of measuring spin-up at $B$ is given by the probability of measuring spin-up along $\vec{B}$ given an electron that was prepared to be spin-up along $\vec{A}$. That's given by: $P = \frac{1}{2} (1 + \vec{A} \cdot \vec{B})$ (I think).

So there's no mystery here. It has a perfectly intuitive "hidden variable" explanation: After the measurement at $A$, the electron is in an eigenstate of $\sigma_{\vec{A}}$, and it stays in that eigenstate until point $B$. The measurement at $B$ gives a probabilistic outcome, but it's a local nondeterministic decision.

Now, look at the same thing from the point of view of the second interpretation:

Here, an $X^0$ particle decays into an electron/positron pair in a state with total angular momentum zero. In this interpretation, measurements $A$ and $B$ are simultaneous (or more generally, at a spacelike separation). But if the measurement of spin at $A$ along axis $\vec{A}$ yields spin-up, then the probability of getting spin-up along $\vec{B}$ at point $B$ is given by:

$P = \frac{1}{2} (1 - \vec{A} \cdot \vec{B})$

which is almost exactly the same (except for the minus sign, which I think is just due to the twisting of the diagram to go from the first interpretation to the second).

The second interpretation leads to the usual spin-1/2 EPR mysteries. The first interpretation is completely non-mysterious. But quantum mechanically, they are described by almost exactly the same mathematics.

I don't really have a coherent question to ask about this, but the similarity of the two processes makes me feel that their explanations should be similar, as well. So either there should be a nonmysterious explanation for the second process, or we should be able to see both of them as equally mysterious.

Any thoughts, or pointers to papers relating EPR to crossing symmetry?

 

[Jilang]

Nice. But why do you feel one process is more mysterious than the other?