If the rock has a spherical symmetry in its mass distribution, it will not start to rotate.
If the rock has no spherical symmetry, it can gain angular momentum, and continue to rotate after it passed the planet. This is easier to show in the limit of large separations, but it stays true in this case as well.
bahamagreen said:
If a spacecraft is in orbit around the planet such that the orientation of the spacecraft is that its belly always faces the planet (the view out the front window will always show the planet below and space above), then the pilot of this craft will measure that he is not rotating - his craft is not tumbling.
An observer floating a ways off will measure the craft as tumbling, making one rotation per orbit.
That is not right, if you measure rotation with a gyrometer (or any other device used to measure rotations) you will get rotation in the first case and no rotation in the second case. You get a wrong impression if you look at the planet - look at the sky or your instruments to see if you are rotating.
bahamagreen said:
Yet, clearly there has been a rotation with respect to the distant stars. So there are really two questions; what really constitutes a rotation and from which vantage point is it being measured
There is an observer-independent way to check if an object rotates.
bahamagreen said:
The rock will see the universe rotate about it during the maneuver
It will not, unless it starts to rotate (=change the alignment of its axes relative to the stars and other objects far away). If it starts to rotate, you can measure it internally in the rock with gyroscopes, you don't need any external reference points.
bahamagreen said:
but will be unable to measure anything local that would be a rotation with respect to its path.
What is "Rotation with respect to its path" supposed to mean?
bahamagreen said:
The floating observer would see the rock begin to slowly rotate so as to keep its same orientation to its orbital path,
This is wrong. Nearly all satellites are counterexamples.
Bandersnatch said:
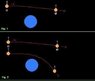
My understanding is that for the rock to rotate synchronously(i.e., the same side always facing the planet) while on a hyperbolic orbit(as in slingshot), angular momentum of the rock's rotation would have to be continuously altered during the approach.
From zero rotation(in an inertial ref.frame) at the infinity from the planet, accelerating to maximum angular velocity at periapsis, and decelerating to zero again during the last leg of the orbit.
The result does not have to be zero.
Baluncore said:
Gravity effects the centre of mass of the rock.
Gravity effects all parts of the rock.
But now consider two rocks, separated, but traveling on different parallel initial paths. Each will travel an independent path. They would have very slightly different final paths after the encounter. So if the rock was now modeled as a long cylinder with two halves, each centred on one of those two points, it would change its astronomical orientation during the pass.
It would also change its angular velocity (in general, the change can be zero as well).