You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Current through a conductor of zero resistance
- Thread starter swap1996
- Start date
-
- Tags
- Conductor Current Resistance Zero
AI Thread Summary
In a circuit with a conductor of zero resistance, current will not flow through a resistor connected to it, as there would be no voltage difference across the resistor. In reality, all wires have some resistance, resulting in a negligible current through the resistor compared to the current through the wires, which can lead to dangerous overheating without current-limiting devices. Superconductors, while having zero resistance, also have limits on the maximum current they can carry, governed by current density and magnetic field constraints. The equivalent resistance between two points in the circuit is determined primarily by the resistors present, with the zero-resistance conductor not contributing. Understanding these principles is essential for analyzing circuit behavior accurately.
Physics news on Phys.org
Nugatory
Mentor
- 15,460
- 10,574
If the wires were really perfect conductors with zero resistance, then there would be no voltage difference between the two ends of the resistor and therefore no current flow through the resistor.
In practice, no wire is a perfect conductor so there's always some tiny resistance and therefore some tiny voltage difference across the resistors to drive some tiny current flow through the resistor. However this current will be well and thoroughly negligible compared with the current through the wires (which will very quickly melt, burn, catch on fire, or explode if there's no fuse, internal resistance in the power supply, or some other current-limiting device).
In practice, no wire is a perfect conductor so there's always some tiny resistance and therefore some tiny voltage difference across the resistors to drive some tiny current flow through the resistor. However this current will be well and thoroughly negligible compared with the current through the wires (which will very quickly melt, burn, catch on fire, or explode if there's no fuse, internal resistance in the power supply, or some other current-limiting device).
Last edited:
Crazymechanic
- 831
- 12
if by the equivalent resistance you mean the total resistance it has with the junctions at both ends then the only resistance in your schematic is the one through "r2"
Nugatory
Mentor
- 15,460
- 10,574
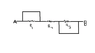
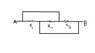
swap1996 said:What is the equivalent resistance between A and B in this case...
Try redrawing that picture so that the resistors are side by side on your sheet of paper... You'll find that this makes the problem much easier.
technician
- 1,506
- 18
Nugatory said:If the wires were really perfect conductors with zero resistance, then there would be no voltage difference between the two ends of the resistor and therefore no current flow through the resistor.
In practice, no wire is a perfect conductor so there's always some tiny resistance and therefore some tiny voltage difference across the resistors to drive some tiny current flow through the resistor. However this current will be well and thoroughly negligible compared with the current through the wires (which will very quickly melt, burn, catch on fire, or explode if there's no fuse, internal resistance in the power supply, or some other current-limiting device).
Where does superconductivity fit in this explanation? I understand that superconductors have zero resistance and currents do flow in suoerconductors
swap1996
- 10
- 0
Nugatory said:Try redrawing that picture so that the resistors are side by side on your sheet of paper... You'll find that this makes the problem much easier.
Can you explain it properly, perhaps upload the diagram you are referring to...
Nugatory
Mentor
- 15,460
- 10,574
technician said:Where does superconductivity fit in this explanation? I understand that superconductors have zero resistance and currents do flow in suoerconductors
There is always some current-limiting device in such a setup, so infinite currents are not observed. But you are right that a superconductor can behave a lot more like an ideal wire than anything you're going to be able buy in a roll and solder together.
Last edited:
Nugatory
Mentor
- 15,460
- 10,574
swap1996 said:Can you explain it properly, perhaps upload the diagram you are referring to...
Not until we've given you a few more hints... This problem is much easier than it looks... The end of every resistor in your diagram is connected directly to either point A or point B.
berkeman
Admin
- 69,110
- 24,027
swap1996 said:Can you explain it properly, perhaps upload the diagram you are referring to...
Even though this is not directly homework, you still need to show some effort here...
Since the left end of R1 is shorted to the right end of R2, just rotate R1 up and over clockwise 180 degrees to put it in parallel with R2. Then do a similar thing with R3 -- rotate it clockwise 180 degrees to put in in parallel with R2. What does the diagram look like now?
technician
- 1,506
- 18
Nugatory said:There is always some current-limiting device in such a setup, so infinite currents are not observed. But you are right that a superconductor can behave a lot more like an ideal wire than anything you're going to be able buy in a roll and solder together.
It was not suggested that the current was infinite !
What 'current-limiting device'do you have in mind?
Last edited by a moderator:
berkeman
Admin
- 69,110
- 24,027
technician said:Where does superconductivity fit in this explanation? I understand that superconductors have zero resistance and currents do flow in suoerconductors
technician said:It was not suggested that the current was infinite !
What 'current-limiting device'do you have in mind?
The maximum current that can be supported by a superconductor is limited either by the current density, or by the magnetic field generated by the current. Above those limits, the superconductor stops being a superconductor, develops some loss, and all hell breaks loose.
This paper from arxiv has some good info: http://www.google.com/url?sa=t&rct=...YReN1mhykYSVQvK0lVOkTmA&bvm=bv.46471029,d.cGE
.
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
As Crazymechanic already pointed out, the equivalent resistance between A and B is R2 .swap1996 said:What is the equivalent resistance between A and B in this case...
For the parallel portions of the circuit:
You can't use ##\displaystyle \ \frac{1}{R_\text{Parallel}}=\frac{1}{R_A}+\frac{1}{R_B} \,,\
## because one of the resistances is zero.
Instead, use ##\displaystyle \ R_\text{Parallel}=\frac{R_A\,R_B}{R_A+R_B} \ .##
Similar threads
- Replies
- 4
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 11
- Views
- 2K
- Replies
- 16
- Views
- 2K
- Replies
- 16
- Views
- 3K
- Replies
- 4
- Views
- 3K
- Replies
- 6
- Views
- 1K
- Replies
- 8
- Views
- 2K
- Replies
- 21
- Views
- 4K
- Replies
- 3
- Views
- 2K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B Simple mass/scale puzzle
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I Solving a momentum problem where masses change after the collision
- Started by rdemyan
- Replies: 35
- Classical Physics
-
B Torque Calculation - Not a basic application
- Started by TeeBeeCee
- Replies: 37
- Classical Physics
-
B Formal definition of work done
- Started by physicals
- Replies: 48
- Classical Physics
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math