KuriousKid
- 48
- 0
- TL;DR
- How current flows in Wide sheet or plate. Is it uniform pattern or something else?
Current flow through a wire is considered (or assumed) to be flown uniform across the cross section of the wire (or is it more near skin? or at core?). However I wonder if that's the case with a sheet or plate or circular disc. e.g. If I apply voltage at two opposite corners of the square or exactly in the middle of the plate. How the current will flow?
I know in transformer the thin plates are used to reduce the eddy current effect, but this is not what I'm tying to understand. I want to know how current will flow through the thick and wide object.
I've attached few options and I was wondering if someone have experimented this and knows the real answer? Assume that Rectangle plate of 3 mm thickness and 18 x 12 inches long/wide is applied AC voltage in the middle as shown below. In first case I showed dotted lines as current flow path... which is parallel to each other across the length of the sheet. In second case, it is somewhat elliptical or something like that. Just try to imagine it as it doesn't reach the corners uniformly but flows as it finds its way in sheet.
Or is there any other pattern, the current will flow? Anyone have idea or have experimented this?
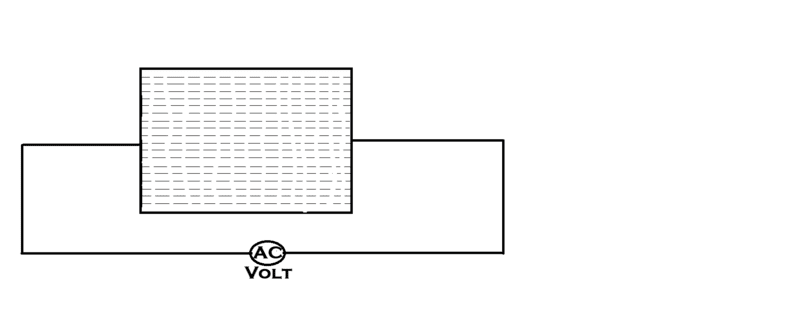
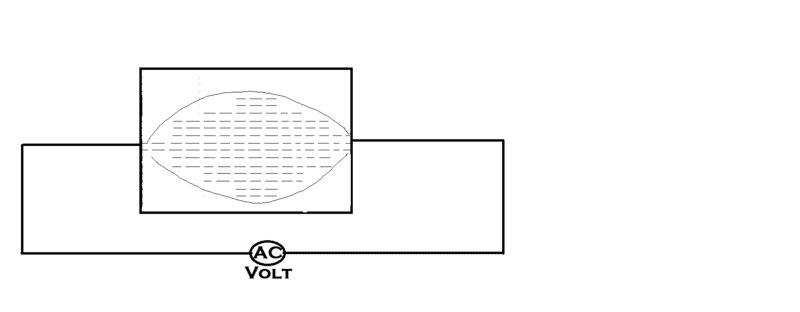
I know in transformer the thin plates are used to reduce the eddy current effect, but this is not what I'm tying to understand. I want to know how current will flow through the thick and wide object.
I've attached few options and I was wondering if someone have experimented this and knows the real answer? Assume that Rectangle plate of 3 mm thickness and 18 x 12 inches long/wide is applied AC voltage in the middle as shown below. In first case I showed dotted lines as current flow path... which is parallel to each other across the length of the sheet. In second case, it is somewhat elliptical or something like that. Just try to imagine it as it doesn't reach the corners uniformly but flows as it finds its way in sheet.
Or is there any other pattern, the current will flow? Anyone have idea or have experimented this?