Cylinder rolling due to magnetic force

[archaic]

Homework Statement

The apparatus in the figure is a distance $h$ from the ground. The cylinder of radius $r$ rolls without slipping. I am asked to find the total horizontal distance that will be travelled until the rod reaches the ground.

Relevant Equations

$$\mathbf{F_B}=I\mathbf L\times\mathbf B$$$$\tau_{net}=I\alpha$$

Hello!

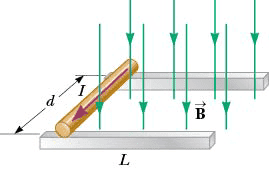
The magnetic force is to the right. $I_c$ is the moment of inertia of the cylinder.
For the net force on the centre of mass, I have the frictional and magnetic forces $F=F_B-f$. I know that $F_B$ is $IdB$.
I also know that $rf=I_c\alpha=I_c\frac ar$, so that $f=I_c\frac{a}{r^2}=\frac{ma}{2}$ (because $I_c=\frac12mr^2$), which gives me $ma=IdB-\frac{ma}{2}\Leftrightarrow a=\frac{2IdB}{3m}\Leftrightarrow F=\frac{2IdB}{3}$.
Using the work energy theorem, I get $\frac12mv^2=\frac23IdBL\Leftrightarrow v=\sqrt{\frac{4IdBL}{3m}}$, which is the horizontal speed when the rod enters free-fall.
The vertical position when the cylinder touches the ground is such that $0=h-\frac12g(\Delta t)^2\Leftrightarrow\Delta t=\sqrt{\frac{2h}{g}}$.
The total range would be $L+v\Delta t=L+\sqrt{\frac{8IdBLh}{3mg}}$
Correct?
Thank you. :)

 

[TSny]

Your work looks correct to me. Instead of using the work-energy theorem, you could have used the kinematic equation $v^2 = v_0^2 +2 a \Delta x$ to find the speed at the start of free-fall.

In your application of the work-energy theorem, someone might ask why you didn't include the rotational KE of the rod. But, your work is correct.

 

[etotheipi]

In your application of the work-energy theorem, someone might ask why you didn't include the rotational KE of the rod. But, your work is correct.

If I'm not mistaken, this is because if the net force on the rod is $\vec{F} = \sum \vec{F}_i = m\ddot{\vec{x}}_{\text{cm}}$, a quantity $\tilde{W}$ defined by$$\begin{align*}\tilde{W} = \int_{\vec{x}_{\text{cm},1}}^{\vec{x}_{\text{cm},2}} \vec{F} \cdot d\vec{x}_{\text{cm}} = \int_{\vec{x}_{\text{cm},1}}^{\vec{x}_{\text{cm},2}} m\ddot{\vec{x}}_{\text{cm}} \cdot d\vec{x}_{\text{cm}} &= \int_{t_1}^{t_2} m \ddot{\vec{x}}_{\text{cm}} \cdot \dot{\vec{x}}_{\text{cm}} dt \\

&= \int_{t_1}^{t_2} \frac{d}{dt} \left( \frac{1}{2} m \dot{\vec{x}}_{\text{cm}}^2 \right) dt \\

&= \Delta \left( \frac{1}{2} m \dot{\vec{x}}_{\text{cm}}^2 \right) = \Delta T_{\text{cm}}

\end{align*}$$which is the change in 'kinetic energy of the centre of mass' only, and not the total change in kinetic energy $\Delta T = \Delta T^* + \Delta T_{\text{cm}}$ where, in this case, $\Delta T^*$ is the change in rotational kinetic energy [i.e. in the centre of mass frame].

The total work done by the Laplace force on all individual mass elements of the rod whilst the rod is rolling along the ramp will be the total change in kinetic energy $W = \Delta T$, and this'll be different to the $\tilde{W}$ from before (which we obtained by multiplying the Laplace force + friction force by the displacement of the centre of mass of the rod). Because the total work done will actually be something like$$W = \sum_i \int_{\vec{x}_1}^{\vec{x}_2} \vec{F}_i \cdot d\vec{x}_i$$where $\vec{F}_i$ is the Laplace force on a small element $m_i$ of the rod somewhere, and $d\vec{x}_i$ the displacement of that small element. E.g the points of the rod currently in contact with the rails have $\dot{\vec{x}}_i = \vec{0}$ and the Laplace force has zero power on them, but the points of the rod currently at the top of the cycle have maximum speed, etc. It would be interesting to see if, if we did the double integral over mass elements in the rod, the total work done by the Laplace force would indeed give us the total change in kinetic energy [including rotational]!

 

[TSny]

It would be interesting to see if, if we did the double integral over mass elements in the rod, the total work done by the Laplace force would indeed give us the total change in kinetic energy [including rotational]!

I don't think it would be very hard to show this. The net work done by all of the elementary Laplace forces (i.e., magnetic forces) acting on the mass elements will turn out to be just the total magnetic force times the distance that the center of mass moves: $IdBL$. And you can check that this equals the total change in translational plus rotational KE of the rod.

 

[archaic]

@TSny thank you very much for your confirmation! I actually forgot about the rotational KE... Glad that it works.
From my textbook, $IdB$ is the force on the whole wire, so I basically thought of the whole cylinder as a point.
Thank you for mentioning that, @etotheipi. I have also asked myself the same question after having read TSny's post.