D'Alembert's principle on a pulley system

[LuccaP4]

Homework Statement

Given the system described in the picture, find the acceleration of every mass using:
a) Newton's equations
b) D'Alembert's principle

Note: Pulley's masses are negligible.

Relevant Equations

$$\displaystyle\sum_{i=1}^N (m_i \ddot r_i - F_i) \delta r_i = 0$$

This is the problem's picture:

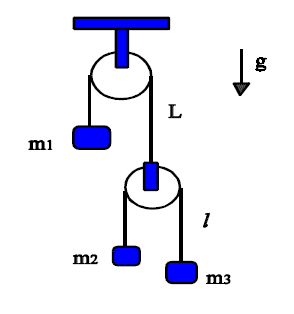
My problem is that what I got for one acceleration (m₃'s) via Newton's equations is not the same as via D'Alembert's principle (I've checked on my PC if they are the same expression).
I can't find the mistake. Any suggestion is welcome.

I attach pictures of what I did:

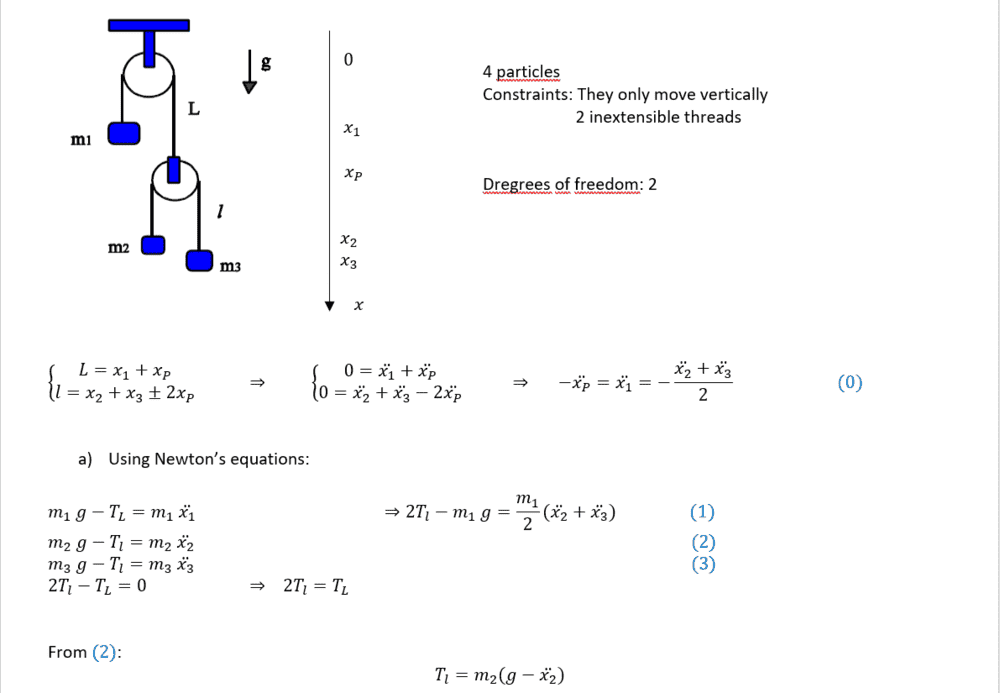
Thank you!

 

[jedishrfu]

Can you post your work in Latex format?

Your writing comes out as very clean and precise but your image quality is very hard to read as they stand.

You can find some directions on the latex markup in a link in my signature below.

 

[LuccaP4]

I struggled just to write the principle on Latex. I'll try uploading a better image.

Edit: It won't let me upload the images because they're too big. Guess I'll type it.

 

[LuccaP4]

Done!

 

[jedishrfu]

That’s great but did you know our site uses Mathjax which means you can write your equations as part of your post using the double # at the front and back of your expression:

$E=mc^2$

# # E = m c^2 # #

removing the spaces between the double # sequence.

 

[LuccaP4]

Thanks for the data! I'll learn it for the next time.

 

[jedishrfu]

Hopefully now one of our physics advisors will respond.

 

[TSny]

It looks like you set up both methods correctly. I did not check all of your work, but I did check to see if your two answers for $\ddot x_3$ match.

Your Newton's law result is

Your D'Alembert result is

When solving the first equation here for $\ddot x_3$, you missed an overall negative sign. (Maybe you just forgot to type it.) Other than that, your two results for $\ddot x_3$ are equivalent.

The result can be simplified to look a little nicer with some manipulations. Try taking your result from Newton's law and combining the terms to make one fraction.

 

[LuccaP4]

Yes, I typed it wrong (copy-paste from above ) but wrote it right. The numerator is negative.
So if they're equivalent, I'll try simplifying the result and go on with the other accelerations.
Thanks for your answer!

 

[LuccaP4]

I solved it, thanks for the help. I attach the entire solution, if anyone is interested.